Author : Thibaut Bernard
Number of visitor

Pythagore
Demonstration of the theorem
|
Author : Thibaut Bernard |
Number of visitor
|
Update: Sunday 30 May 2001.
Alphaquark author's Note :
This page is a translation of
Démonstration du théorème de Pythagore
with the help of
Altavista translation.
I hope this translation is good, but if there are any errors, you can
write me.
If this translation is successful, perhaps I will try to translate another document of
Alphaquark.

Construction of the geometrical figure which will be used for the demonstration
Let us take a rectangle of width A and height B. This rectangle which we make swivel of 90o in the following way :
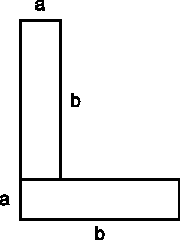
|
For each rectangle, let us divide into two in the following way : |
|
|
|
Let us make swivel of 90o the right-angled triangles in the following way yellow and purple : |
|
|
|
|
|
|
|
We thus find ourselves with four right-angled triangles. |
|
|
|
We note that one finds oneself with a square inside another. |

Demonstration
Notation
Let us take again our last diagram to indicate each of with dimensions by the following letters:
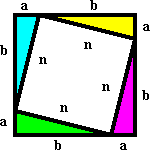
One has four right-angled triangles of which :
the with dimensions one opposed by a,
the base is indicated by b,
and the hypotenuse by n.
Each hypotenuse n thus represent dimensions small square.
With dimensions opposite more the base (a + b) of each right-angled triangle represent each one of with dimensions great square.
Surface squares
Small square : n2.
Great square : (a + b)2.
Surface right-angled triangles
If one associates two right-angled triangles, one finds oneself with a rectangle of surface : a * b.
The total surface of the four right-angled triangles is : 2ab.
Difference in surface
The surface of the small square is equal to the surface of the great square minus the surface of the four right-angled triangles :
n2 = (a + b)2 - 2ab
from where
n2 = a2 + 2ab + b2 - 2ab
what gives
n2 = a2 + b2
Conclusion, the square on the hypotenuse is equal to the sum of the squares of with dimensions of the right angle.