 This is the equation for an ellipse:
This is the equation for an ellipse:
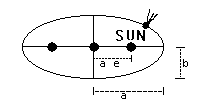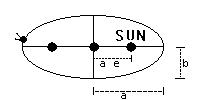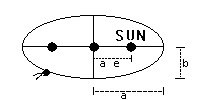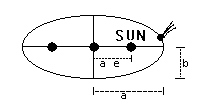
LAW 1: The orbit of a planet/comet about the Sun is an ellipse with the Sun's center of mass
at one focus
 This is the equation for an ellipse:
This is the equation for an ellipse:
![]()
LAW 2: A line joining a planet/comet and the Sun sweeps out equal areas in equal intervals of time
Click here to see larger animation
LAW 3: The squares of the periods of the planets are proportional to the cubes of their semimajor axes:
| Planet | P (yr) | a (AU) | T2 | R3 |
|---|---|---|---|---|
| Mercury | 0.24 | 0.39 | 0.06 | 0.06 |
| Venus | 0.62 | 0.72 | 0.39 | 0.37 |
| Earth | 1.00 | 1.00 | 1.00 | 1.00 |
| Mars | 1.88 | 1.52 | 3.53 | 3.51 |
| Jupiter | 11.9 | 5.20 | 142 | 141 |
| Saturn | 29.5 | 9.54 | 870 | 868 |
 | Johannes Kepler (1571-1630) |  |
Halfway through the thirteenth century, after Greek manuscripts of Arabic science had been translated into Latin for study in European universities, knowledge of astronomy had spread throughout Europe. The Renaissance blossomed in the next two centuries, ushering in a new era in picturing the physical world, ending the dominance of ecclesiastical concerns. The reformation had challenged the authority of church hierarchy with "Sola Scriptura" (ie Only the Scriptures). In the atmosphere of this new intellectual freedom of thought, Copernicus came up with a simplified geometrical system of looking at the universe.
When the the Renaissance and the Reformation were coming to an end in the years prior to 1600, Copernicus's work was read by a few astronomers who recognized the computational advantages of the Copernican system. However, they were not willing to take seriously its philosophical and physical implications.
Enter Johannes Kepler! Johannes Kepler (1571-1630), the German assistant and successor to Tycho Brahe, was a Copernican from his twenties on, and was destined to bring about acceptance of the heliocentric concept. That is, he believed the sun rather than the earth was the center of the planetary system.
The life-long question that concerned Kepler was the nature of the timing and motion of the celestial machinery, for he was convinced that simple mathematical relations existed that could make sense of the planetary system. He saw the planetary system operating according to its own set of mathematical laws which was quite a radical idea for those times.
Kepler was a mathematician rather than an observer. Yer, Kepler was supplied with years of impeccable data by the elder Tache Brahe who had carefully marked the position of Mars in relationship to the rest of the celestial map. Kepler rejected many ideas, such as circular orbits, because they did not fit Brahe's observations. In 1609, Johannes Kepler finally published his first two laws of planetary motion in a book entitled New Astronomy. A decade later (1619), his third law was published in The Harmonies of the World.
| "By the study of the orbit of Mars, we must either arrive at the secrets of astronomy or forever remain in ignorance of them." Johannes Kepler |
Through these works, Kepler can be seen in many respects to mark the beginnings of what we call modern science. Kepler developed his empirical laws from Brahe's data on Mars: "By the study of the orbit of Mars," he said, "we must either arrive at the secrets of astronomy or forever remain in ignorance of them." However, in what proved to be a revolutionary step, Kepler then generalized saying that his laws applied to all the planets, including the Earth, without ever actually verifying that this was indeed true. Now we now know, they even apply to comets. Though Kepler may not have dreamed of such things, the generalization of his laws predict and explain the motion of satelites orbiting the earth. The expectation that the mathematical laws of science are universal is so readily accepted in our time that it is difficult to imagine just how important to science Kepler's actions were.
Kepler's work put to rest any notion that planets move in perfectly circular orbits because nature has decreed that the heavenly bodies must show perfection in their movements. He also put to rest in the scientific community an ancient idea that there exists a mystical complex motion of planets that somehow governs our ways. Although Kepler never knew why planets move by the empirical relationships articulated in his three laws, he diligently sought a cause of which these three laws were the effect. As he stated, "I am much occupied with the investigation of physical causes. My aim in this is to show that the celestial machine is ...... rather a clockwork..."; Kepler vaguely sensed that bodies have a natural "magnetic" affinity for each other and guessed that the Sun has an attractive force. However, it remained for Newton, half a century later, to formulate a unified theory of motion involking gravity as the cause of planetary motion.
 | Tycho Brahe (1546-1601) |  |
Without the diligent work of Tycho Brahe, Kepler would not have had the accurate data of Mars from which he derived his famous three laws.
Appearing at an opportune time, the right man for the next advance in astronomy was Danish nobleman-astronomer Tycho Brahe. With the financial might of King Frederick II, Brahe constructed an observatory on the island of Hveen, about 32 km northeast of Copenhagen, in 1582. With the most accurate pretelescopic observing instruments ever designed, Brahe determined positions with a precision of 1 minute of arc, far surpassing any previous measurements. He was the first to observe and record the positions of the Sun, Moon, planets, and stars with regularity. In the past, this was done haphazardly, at best. He faithfully recorded their movements over many years, making them available for future study.
Brahe had reservations about adopting the heliocentric theory of Copernicus. He accepted the idea that the five known planets revolved around the Sun, but not the idea that the earth moved. It was far too heavy and sluggish. The earth's motion would be felt, he argued. Most important to Brahe, a moving Earth was contrary to scriptural belief. In addition, he was unable to detect the Earth's orbital motion by parallactic shifts in the positions of the brighter stars. Thus, the cosmological system of Brahe was a complex compromise: The planets orbited the Sun; the Sun and Moon, in turn, orbited a fixed Earth. It was a mathematical nightmare! There was relatively little interest in Brahe's cosmology, and it was never seriously considered.
Brahe's great contribution in science came not from his ideas but from the persistance, consistance, and accuracy with which he recorded the position of the planet, Mars. From this accurate taking of data, Kepler could derive his famous laws.
Kepler was fortunate. His sound faith in a heliocentric solar system with geometric simplicity proved correct. He was able to explain the motion of all orbiting bodies through the manipulation of data from only one (Mars). He never tested his hypothesis on the other planets, but we now know that it holds true for all orbiting bodies.
Brahe was less fortunate in his theories. Brahe's beliefs are a classic case where wrong conclusions can be obtained from accurate data. In his case, poor theology prevented good science. There is a lesson to learn here. However, one must also be careful not to take that warning to the extreme. One could also corrupt sound theology with poor science.