


KEPLER'S LAWS OF
PLANETARY MOTION
I
PLANETS MOVE IN ELLIPTICAL ORBITS AROUND THE SUN, WHICH OCCUPIES
ONE FOCUS OF THE ELLIPSE
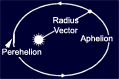
An ellipse is a flattened circle whose
properties are governed by two 'foci', or focal points, equidistant from its centre. The line joining the Sun and a planet (the radius vector) varies in length at different
points on its orbit
2
THE RADIUS VECTOR SWEEPS OUT
EQUAL AREAS IN EQUAL TIMES
The radius vector is shortest when the planet is at perihelion and longest at aphelion. No
matter where the planet is in its orbit, however, the area of the ellipse covered by the radius
vector will be the same over a given period of time. The shaded areas in the diagram are equal and the planet takes the same
period of time to cover them, yet the distance it travels along its orbit varies.

3
THE SQUARE OF THE TIME TAKEN BY
EACH PLANET TO COMPLETE ITS ORBIT
IS PROPORTIONAL TO THE CUBE OF
ITS MEAN DISTANCE FROM THE SUN
This can be illustrated with the example of
Saturn. The year (i.e. the period of the
Earth's orbit of the Sun) represents one unit of time. The Earth's mean distance from the Sun represents one unit of distance. Saturn takes approximately 27 years to complete its orbit. 27x27 (the square of the time) gives 729. The cube root of 729 is 9. Saturn's mean
distance from the Sun is roughly 9 times
that of the Earth.
| |
|
 |
"The heavenly motions... are nothing but a continuous song for several voices,
perceived not by the ear but by the intellect,
a figured music which sets landmarks
in the immeasurable flow of time."
John Banville: Kepler, (Minerva 1990)
Kepler's Background
Johannes Kepler was born on 6th January 1572 (NS) at Weil-der-Stadt in the German province of Swabia. His grandfather had been mayor of the town but the Kepler family fortunes were in decline. His father was a bullying adventurer who earned a precarious living as a mercenary soldier and deserted the family when Johannes was 17. His mother, an inn-keeper's daughter, had a reputation for witchcraft.
Born prematurely, Johannes was weak and sickly. He spent a solitary, unhappy childhood, but at least he was fortunate in that the ruling Dukes of Württemburg had created a relatively enlightened system of education in Swabia. With a view to recruiting the brightest minds for the Protestant clergy, a system of grants and scholarships was available to promising (male) children of poor families, and despite his ill health, Johannes was precociously brilliant.
His schooldays, though academically successful, were thoroughly miserable. His know-all cleverness irritated his classmates, who frequently beat him up. He considered himself physically repulsive (admitting to 'a dog-like horror of baths'), thoroughly unlikeable, an outsider. He turned to the world of ideas for escape and found solace in an abiding religious conviction.
In 1587 Kepler went to Tübingen University where he proved to be an excellent mathematician. He also became an advocate of the controversial Copernican theory of the solar system, which he often defended in public debates. At that time Kepler was not particularly interested in astronomy. The idea of a Sun-centred universe had a mystical appeal. He intended to become a clergyman and when he graduated in 1591 he entered the Tübingen faculty of theology. Before taking his final examinations, however, he was recommended for the vacant post of teacher of mathematics and astronomy at the Protestant school at Graz in Austria, which he took up in April 1594, aged 23. There were no clear distinctions between astronomy and astrology; amongst his duties as 'mathematicus' Kepler was expected to issue an annual almanac of astrological predictions. In his first almanac he predicted an exceptionally cold winter and a Turkish incursion into Austria. When both predictions proved correct, he unexpectedly gained a reputation as a prophet.
The Cosmic Mystery
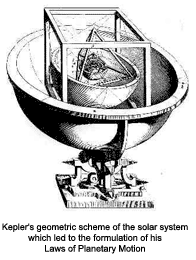
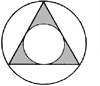 On 19th July 1595 (NS), a sudden revelation changed the course of Kepler's life. In preparation for a geometry class he had drawn a figure on the blackboard of an equilateral triangle within a circle with a second circle inscribed within it. He realised that the ratio of the two circles replicated the ratio of the orbits of Jupiter and Saturn. In a flash of inspiration, he saw the orbits of all the planets around the Sun arranged so that regular geometric figures would fit neatly between them. He tested this intuition using two-dimensional plane figures ? the triangle, square, pentagon, etc. ? but this didn't work. As space is three-dimensional, he went on to experiment with three-dimensional geometric solids. On 19th July 1595 (NS), a sudden revelation changed the course of Kepler's life. In preparation for a geometry class he had drawn a figure on the blackboard of an equilateral triangle within a circle with a second circle inscribed within it. He realised that the ratio of the two circles replicated the ratio of the orbits of Jupiter and Saturn. In a flash of inspiration, he saw the orbits of all the planets around the Sun arranged so that regular geometric figures would fit neatly between them. He tested this intuition using two-dimensional plane figures ? the triangle, square, pentagon, etc. ? but this didn't work. As space is three-dimensional, he went on to experiment with three-dimensional geometric solids.
Ancient Greek geometers knew that the number of solids that can be constructed from regular geometric figures is limited to five. They are known variously as the 'perfect', 'Pythagorean' or 'Platonic' solids. Kepler speculated that one of the five solids could be inserted between each concentric planetary sphere. This seemed to explain why there were just six planets (Mercury, Venus, Earth, Mars, Jupiter, Saturn) with five intervals separating them, and why the intervals were so irregular. Convinced that he had discovered a subtle geometric relationship between the diameters of the planetary orbits and their distances from the Sun, Kepler wrote Mysterium Cosmographicum ('the cosmic mystery'), published in 1596. The scheme worked reasonably well with the planetary distances then accepted, but even Kepler could see that it wasn't perfect. Assuming that better data on planetary orbits would bear out his theory, he devoted the rest of his life to justifying his vision through scientific observation and hard mathematical proofs.
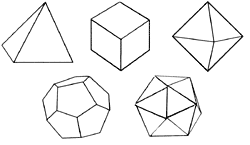
The five 'Platonic' solids:
the tetrahedron (comprising four triangles);
the cube (six squares);
octohedron (eight triangles);
dodecahedron
(twelve pentagons)
and
isosahedron
(twenty triangles) |
In pursuing his quest to pin down the cosmic mystery, Kepler transcended formidable obstacles in his personal and professional life and rose to become one of the immortal names in European astronomy. [1]
His greatest achievement was the formulation of the Laws of Planetary Motion which made a fundamental break with astronomical tradition in describing the orbits of the planets as elliptical rather than circular and in recognising that a planet's speed is not uniform but varies at different stages of its orbit. The first two Laws were announced in l609 in Astronomia Nova ('the new astronomy'). It took a further nine years to formulate the Third Law which established a relationship between a planet's distance from the Sun and the time it takes to complete an orbit. This was announced in Harmonice Mundi ('harmony of the world'), published 16l8. Collectively Kepler's Laws superseded the ancient Ptolemaic concept of a spherical universe with epicyclic motion. They provided the foundation upon which Isaac Newton was to build his epoch-making theory of universal gravitation towards the end of the 17th century.
To Kepler himself, however, the planetary laws represented far more than the description of a physical mechanism. In the tradition of the legendary Greek philosopher Pythagoras (6th century BC), Kepler did not view science and spirituality as mutually exclusive. The deeper significance of Kepler's Laws is that they reconcile the emerging vision of a Sun-centred planetary system with the ancient Pythagorean concept of armonia, or universal harmony.
Celestial Harmony
Pythagoras discovered that the pitch of a musical note depends upon the length of the string which produces it. This allowed him to correlate the intervals of the musical scale with simple numerical ratios. When a musician plays a string stopped exactly half-way along its length an octave is produced. The octave has the same quality of sound as the note produced by the unstopped string but, as it vibrates at twice the frequency, it is heard at a higher pitch. The mathematical relationship between the keynote and its octave is expressed as a 'frequency ratio' of 1:2. In every type of musical scale, the notes progress in a series of intervals from a keynote to the octave above or below. Notes separated by intervals of a perfect fifth (ratio 2:3) and a perfect fourth (3:4) have always been the most important 'consonances' in western music. In recognising these ratios, Pythagoras had discovered the mathematical basis of musical harmony.
In one sense Pythagoras had also invented western science. By associating measurements of length with musical tones he made the first known reduction of a quality (sound) into a quantity (length and ratio). The understanding of nature through mathematics remains a primary objective of science today. But Pythagoras also recognised that the musical octave is the simplest and most profound expression of the relationship between spirit and matter. The 'miracle of the octave' is that it divides wholeness into two audibly distinguishable parts, yet remains recognisable as the same musical note ? a tangible manifestation of the hermetic maxim 'as above, so below'. The short-lived but profoundly influential Pythagorean Brotherhood sought to unite "religion and science, mathematics and music, medicine and cosmology, body, mind and spirit in an inspired and luminous synthesis". [2]
The Pythagoreans used music to heal the body and to elevate the soul, yet they believed that earthly music was no more than a faint echo of the universal 'harmony of the spheres'. In ancient cosmology, the planetary spheres ascended from Earth to Heaven like the rungs of a ladder. Each sphere was said to correspond to a different note of a grand musical scale. The particular tones emitted by the planets depended upon the ratios of their respective orbits, just as the tone of a lyre-string depended upon its length. Another type of celestial scale related the planetary tones to their apparent rates of rotation around the Earth. The music of the spheres was never a fixed system of correspondences. Many variant schemes existed because each philosopher would necessarily approach it from a slightly different perspective. The musicologist Joscelyn Godwin comments, "...the celestial harmony of the solar system... is of a scope and harmonic complexity that no single approach can exhaust. The nearest one can come to understanding it as a whole is to consider some great musical work and think of the variety of analytical approaches that could be made to it, none of them embracing anything like the whole." [3]
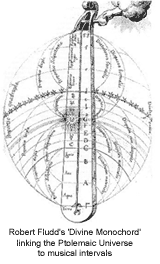 Plato, Pliny, Cicero and Ptolemy are amongst the philosophers of the ancient world who contemplated the music of the spheres. The doctrine was transmitted to medieval Europe where it found its most glorious expression in the architecture of great abbeys and cathedrals consciously designed to conform to the proportions of musical and geometric harmony. The English hermeticist Robert Fludd (1574-1637) visualised grand celestial scales spanning three octaves and linking levels of existence from the sub-planetary elemental worlds to exultant choirs of angelic intelligences beyond the stars. The beautiful engravings which illustrate Fludd's encyclopaedic works are amongst the most comprehensive descriptions of pre-Copernican cosmology ever devised. [4] Plato, Pliny, Cicero and Ptolemy are amongst the philosophers of the ancient world who contemplated the music of the spheres. The doctrine was transmitted to medieval Europe where it found its most glorious expression in the architecture of great abbeys and cathedrals consciously designed to conform to the proportions of musical and geometric harmony. The English hermeticist Robert Fludd (1574-1637) visualised grand celestial scales spanning three octaves and linking levels of existence from the sub-planetary elemental worlds to exultant choirs of angelic intelligences beyond the stars. The beautiful engravings which illustrate Fludd's encyclopaedic works are amongst the most comprehensive descriptions of pre-Copernican cosmology ever devised. [4]
The ideals of Pythagorean harmony inspired Copernicus himself. Nicholas Copernicus (1473-1543) spent most of his life in the fortified city of Frauenburg in Prussia fulfilling administrative duties as a canon of the cathedral chapter and devoting the rest of his time to contemplation of the cosmic harmonies. The cumbersome mathematics of the Ptolemaic system, with its maze of epicycles grafted on to reconcile various observational discrepancies, offended his Pythagorean sense of proportion. He realised that a Sun-centred planetary system not only gave better predictions of celestial motion but could also he expressed through more elegant geometry ? to the greater glory of God the Creator.
Kepler's early enthusiasm for the Copernican system was inspired by the same sense of idealism. He could readily accept the Sun as the centre of the planetary system, but the necessity of rejecting circular orbits came as something of a shock. The circle is an archetypal symbol of harmony and perfection; Kepler recoiled with disgust when an unsightly bulge began to emerge from his analysis of the orbit of Mars. Yet the elliptical orbits eventually revealed a scheme of celestial harmony more subtle and profound than any that had gone before.
Kepler's, First Law states that the planets move in ellipses and that the Sun is not at the exact centre of their orbits. Each planet moves between a 'perihelion' point nearest the Sun and an 'aphelion' point furthest away. The Second Law states that the planets move faster at perihelion than at aphelion. Kepler measured their angular velocities at these extremes (i.e. how far they travel in 24 hours in minutes and seconds of arc as viewed from the Sun) and expressed this ratio as a musical interval. Saturn, for instance, moves at a rate of 106" per day at aphelion and l35" at perihelion. Cancelled down, the ratio 106:135 differs by only two seconds from 4:5 ? equivalent to the interval of a major third. Kepler found that the angular velocities of all the planets closely correspond to musical intervals. When he compared the extremes for combined pairs of planets the results were even more marvellous, yielding the intervals of a complete scale. Thus, the ratio between Jupiter's maximum and Mars' minimum speed corresponds, to a minor third; the interval between Earth and Venus to a minor sixth. Rather than the fixed-tone planetary scales of earlier schemes, Kepler's measurements revealed ever-changing polyphonic chords and harmonies as the planets move between perihelion and aphelion. Furthermore, he had shifted the focus of celestial harmony from the Earth to the Sun: "Henceforth it is no longer a harmony made for the benefit of our planet, but the song which the cosmos sings to its lord and centre, the Solar Logos". [5]
Scientific materialists have tended to dismiss the spiritual dimension to Kepler's work as either the remnants of a deeply-ingrained 'medievalism' which he was unable to shake off or, even less charitably, as the fantasies of an over-worked mind. His vision of the music of the spheres, however, is based upon the hard facts of astronomical measurement. The astronomer Fred Hoyle agrees that the correspondence between musical ratios and planetary velocities as described by Kepler is "frighteningly good". [6]
The Kepler scholar Francis Warrain extended Kepler's researches and found that the angular velocities of Uranus, Neptune and Pluto, which were unknown during Kepler's lifetime, also correspond to harmonic ratios. The music of the spheres is more than a beautiful poetic intuition. The dynamics of the solar system, first laid bare by Kepler's mathematical genius, are directly analogous to the laws of musical harmony.
Kepler and Astrology
Although he first became famous for the accuracy of his predictions and scored an impressive number of 'hits' during his career, Kepler's attitude to conventional astrology was ambivalent and complex. In attempting to disentangle it, we can at least begin by dismissing the notion that he rejected astrology out-of-hand. In the official history of scientific progress, the values of the Age of Reason and Industrial Revolution were projected onto the brilliant mathematician who had unravelled the laws of planetary motion. It seemed inconceivable that he could be tainted with the medieval superstition of astrology. Like Isaac Newton's passion for alchemy and theology, this aberration was best glossed over or, as actually happened in Kepler's case, twisted into a distortion of the truth.
Kepler's famous metaphor comparing astrology to the 'foolish daughter' of the 'wise mother' (astronomy) has often been cited as evidence of his disbelief. Seen in context, however, the foolish daughter represents a particular style of astrology ? popular astrology ? which was not to Kepler's taste. He was always careful to distinguish his reverential vision of the celestial harmonies from the practices of the backstreet astrologers and almanac-makers "who prefer to engage in mad ravings with the uneducated masses".[7]
Kepler's astrology was on another plane altogether. Before condemning him for his blatant intellectual snobbery, however, consider how many 'serious' astrologers today feel exactly the same way about Sun-sign columns. Kepler was neither the first nor the last astrologer to pour scorn on those who practise apparently inferior forms of the art. His disapproval stems from his conviction that astrology is nothing less than a divine revelation, "...a testimony of God's works and... by no means a frivolous thing". Unfortunately, Kepler's salary as Imperial Mathematicus was rarely paid (the Imperial treasury owed him 20,000 florins by the end of his career) so he was obliged to scratch out a living by giving astrological advice to wealthy clients and composing astrological almanacs for the 'uneducated masses' he so despised. Reluctantly, Kepler conceded that "the mother would starve if the daughter did not earn anything". In another famous turn of phrase, he warned those learned professors who had grown sceptical of astrology that they were likely to "throw the baby out together with the bathwater" if they rejected it entirely.
So Kepler was undoubtedly an astrologer ? but he was no respecter of astrological tradition. His ideas seem radical even by the standards of mainstream astrology today. For a start, he dismissed the use of the 12 houses as 'Arabic sorcery'. While accepting that the angles were important, he could see no justification for conventional house division. "Demonstrate the old houses to me," he wrote to one of his correspondents, "Explain their number; prove that there can be neither fewer nor more... show me undoubted and striking examples of their influence." [8]
He even went so far as to question the validity of the signs of the zodiac, arguing that they were derived from human reasoning and arithmetical convenience rather than any natural division of the heavens.[9] He had no time for elaborate schemes of planetary sign rulership and saw no reason why some planets should be classed as benefic and others as malefic.
Kepler left no astrological convention unchallenged. His rigorous questioning hints at a massive reformation of astrology, on a scale which Ken Negus has compared to the reformation that Martin Luther brought about in the Church. Kepler's great attempt to purge astrology seems to echo the Pythagorean katharsis ? a frenzied purification of the soul undertaken in order to restore divine harmony. More prosaically, it should be seen in the context of the monumental changes taking place in theoretical astronomy during the 16th and 17th centuries. The ancient Aristotelian doctrines that had given astrology some measure of scientific credibility were crumbling fast. Copernicus had displaced the Earth from the centre of the universe; Tycho had proved that the 'immutable' heavens were subject to change as new stars blazed in the sky; Galileo's telescope had opened up dimensions undreamt of by Ptolemy; Kepler himself had shattered the serene, circular motions of the planetary orbits forever. He sensed that astrology would have to adjust to the new astronomy if it were to keep pace with the march of science.
The New Aspects
The key to Kepler's proposed reform is his approach to the aspects. Traditional astrology recognises five significant relationships, based upon the twelvefold division of the zodiac signs. Ptolemy taught that their significance was derived by analogy with the ratios of the musical scale.[10] The conjunction is equivalent to the same two notes played in unison. The opposition divides the circle in the ratio 1:2, which corresponds to the octave. The sextile (5:6) corresponds to a minor third, the square (3:4) to a perfect fourth and the trine (2:3) to a perfect fifth. By placing less emphasis upon the zodiac signs, however, Kepler was free to explore additional aspect relationships in his pursuit of the Pythagorean synthesis of music, geometry and astronomy.
 Kepler's new aspects were based upon harmonic theory and grounded in empirical observation of astrological effects. From his long-term study of weather conditions correlated with planetary angles and from detailed analysis of his collection of 800 birth charts, Kepler concluded that when planets formed angles equivalent to particular harmonic ratios a resonance was set up, both in the archetypal 'Earth-soul' and in the souls of individuals born under those configurations. [11] He considered this 'celestial imprint' more important than the traditional emphasis on signs and houses: "in the vital power of the human being that is ignited at birth there glows that remembered image..." The geometric-harmonic imprint constitutes "the music that impels the listener to dance" as the movements of the planets, by transit and direction, echo and re-echo the natal theme. In addition to the Ptolemaic aspects, Kepler proposed the quintile (72°), bi-quintile (144°) and sesqui-quadrate (135°). Extending the analogy of the musical scale, the quintile is equivalent to an interval of a major third (4:5), the sesqui-quadrate to a minor sixth (5:8) and the bi-quintile to a major sixth (3:5). Kepler's new aspects were based upon harmonic theory and grounded in empirical observation of astrological effects. From his long-term study of weather conditions correlated with planetary angles and from detailed analysis of his collection of 800 birth charts, Kepler concluded that when planets formed angles equivalent to particular harmonic ratios a resonance was set up, both in the archetypal 'Earth-soul' and in the souls of individuals born under those configurations. [11] He considered this 'celestial imprint' more important than the traditional emphasis on signs and houses: "in the vital power of the human being that is ignited at birth there glows that remembered image..." The geometric-harmonic imprint constitutes "the music that impels the listener to dance" as the movements of the planets, by transit and direction, echo and re-echo the natal theme. In addition to the Ptolemaic aspects, Kepler proposed the quintile (72°), bi-quintile (144°) and sesqui-quadrate (135°). Extending the analogy of the musical scale, the quintile is equivalent to an interval of a major third (4:5), the sesqui-quadrate to a minor sixth (5:8) and the bi-quintile to a major sixth (3:5).
Kepler realised that many more aspect configurations are possible, but rejected them on aesthetic grounds. The Ptolemaic aspects and his three new ones gave a pleasing correspondence with the consonances of the musical scale, other aspect ratios produced only discord. The mathematical principles of musical harmony are directly related to geometry ? which Goethe described as 'frozen music'. Kepler rejected aspects based upon geometric figures like the 7-sided septagon and 9-sided nonagon because they cannot be constructed with straight-edge and compasses ? the only instruments permissible in classical geometry. He regarded such figures as 'unknowable' and declared that "God did not employ the septagon and other figures of this species to embellish the world."[12]
The new aspects were soon adopted by astrologers, though perhaps not in quite the spirit that Kepler would have wished. William Lilly wrote Christian Astrology in 1647, less than 20 years after Kepler's death. In the section on the 'Effects of Directions', Lilly gives instructions for finding not only the quintile, bi-quintile and sesqui-quadrate, but also the semi-sextile (30°), semi-quintile (36°), semi-quadrate (45°) and sesqui-quintile (108°). His lengthy analysis of the directions in the chart of 'an English merchant' gives some early examples of the new aspects in practical interpretation.[13] The direction of the Midheaven to sesqui-quadrate Mars, for instance, "may endanger, in some small measure, our Native's repute with false aspersions". The Ascendant to quintile Mercury suggests that he "should now have rectified his books of accounts and receive much benefit from Mercurial men". The quintile-based aspects emerge as 'mildly beneficial' in their effects; the quadrate-based as 'slightly harmful' ? which became the standard textbook interpretation of the 'minor aspects' from Lilly's time to the present.
More in line with Kepler's radical approach are the teachings of the 20th century Hamburg School which originated in l913 when the amateur astrologer Alfred Witte (1878-1941) was invited to give a talk to the Hamburg Kepler Circle.[14] Witte's system of 'planetary pictures', based upon midpoint combinations, was developed by Rheinhold Ebertin (1901-88), author of the indispensable Combination of Stellar Influences. The spirit of Kepler can also be glimpsed in harmonic astrology as developed by John Addey (1920?82), though with the interesting distinction that where Kepler looked to musical scales and harmonies, Addey's harmonic wave-forms are more suggestive of rhythm and tempo.
Though rarely articulated, the concept of universal harmony flows like an underground current through the philosophy of astrology down the ages. In this sense Johannes Kepler, the first 'modern' astrologer, belongs to a broader tradition which links such apparently diverse thinkers as Pythagoras and Ptolemy, Robert Fludd and John Addey, Gurdjieff and Rudolph Steiner. No-one can claim a monopoly on truth. Every astrologer, regardless of style or technique, is attuned to their own unique variation on the 'song of the angels', the all-pervading music of the spheres.
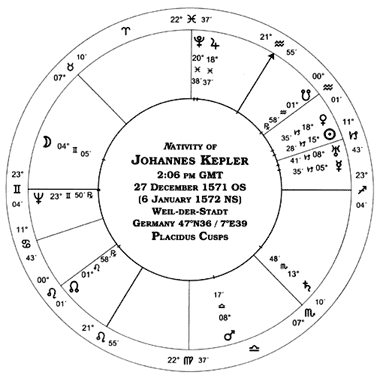 Please note:
Please note:
Larry Ely argues that the above chart is incorrect. In a message left in the guestbook he writes: "He was born in Weil der Stadt, whose coordinates are 48n45; 8e53. Kepler gave his birth time as 2:30 pm in Arthur Koestler, The Watershed. That time is Sun Time, or Local Apparent Time. The corresponding UT is aproximately 14:01. The Mideaven is 21Aq54 and the Ascendant is 24Ge19. Kepler said his MC was in the 22nd degree of Aquarius, and his AS was in the 25th degree of Gemini, so his given time of 2:30 pm checks out. His angles may be need to be rectified by perhaps up to 15' arc, but judging from some events and from a time composite to my chart, the angles above are accurate to about 5' arc, I think."
Notes & References:
| |
1 ] |
The standard biography is Kepler by Max Caspar, translated by C. Doris Hellman (Collier-Mac, 1962). Try your local library. More readily available is Arthur Koestler's The Sleepwalkers (Peregrine Books, 1988) which contains a detailed study of Kepler' s troubled life and the development of his ideas. Also recommended is John Banville' s historical novel Kepler cited above.
Back to text
|
|
| |
2 ] |
Koestler, op cit. p. 27
Back to text
|
|
| |
3 ] |
Joscelyn Godwin: Harmonies of Heaven and Earth (Thames and Hudson 1987), p.130
Back to text
|
|
| |
4 ] |
For an annotated collection of Fludd's most important plates, see Robert Fludd: Hermetic Philosopher and Surveyor of Two Worlds by Joscelyn Godwin (Thames and Hudson 1979). Kepler and Fludd corresponded with one another, but Fludd regarded Kepler's mathematical approach to cosmology as superficial, while Kepler regarded Fludd's magical approach as superstitious.
Back to text
|
|
| |
5 ] |
Harmonies of Heaven and Earth p.145
Back to text
|
|
| |
6 ] |
Quoted in 'Kepler's Belief in Astrology' by Nick Kollerstrom. History and Astrology edited by A. Kitson (Unwin 1989), p.167.
Back to text
|
|
| |
7 ] |
Quoted in Kepler's Astrology: Excerpts, selected, translated and edited by Ken Negus (Eucopia Publications 1987). Unless otherwise stated, all quotes by Kepler himself are from this compilation.
Back to text
|
|
| |
8 ] |
From a letter to the astronomer David Fabricius quoted in Neo-Astrology: a Copernican Revolution by Michel Gauquelin (Arkana 1991), p.92
Back to text
|
|
| |
9 ] |
Kepler later qualified his criticism of the zodiac signs by remarking that, "...the human race has envisioned this partition from the time of the Chaldeans down to our own time". This being so, he wondered whether "God himself does not conform to it... and whether He does not wish to speak to human beings therewith in a language or method of communication that they understand".
Back to text
|
|
| |
10 ] |
Ptolemy: Tetrabiblos (Loeb) p.73-5. In Ptolemy's unfinished Harmonics, he proposed the earliest known 'tone-zodiac', linking the 12 signs to musical intervals. This idea has been explored by other astro-musical theorists, notably Rudolph Steiner.
Back to text
|
|
| |
11 ] |
Kepler' s belief in the ancient doctrine that the Earth as a whole may be regarded as a living entity is echoed in the 'Gaia principle' popularised by James Lovelock during the 1980s.
Back to text
|
|
| |
12 ] |
Koestler op. cit. p.396
Back to text
|
|
| |
13 ] |
William Lilly: Christian Astrology (1647, Regulus reprint 1984), p.785 et seq.
Back to text
|
|
| |
14 ] |
M. Harding and C. Harvey: Working with Astrology (Arkana 1990), p.11.
Back to text
|
|
David Plant is a respected scholar of the history and traditional practice of astrology. He is also an expert on the English Civil War period and the life and work of the 17th century astrologer William Lilly. He runs two very reputable websites: the
English Merlin site, which is devoted to all aspects of the life and times of
William Lilly and his contemporaries; and the British Civil Wars and Commonwealth site, which explores the turmoil of the Civil Wars and Interregnum, and the constitutional experiments of the Commonwealth and Protectorate period of the 1650s.
Both sites are leading points of reference for their fields and a visit is strongly recommended.
© David Plant
|  |
http://www.skyscript.co.uk
|
| |
Read about the life & work of:
|



