

Johannes Kepler :
The Renaissance astronomer and astrologer Johannes Kepler is best known for his discovery of the three principles of planetary motion, by which he clarified the spatial organization of the solar system. Moreover, he founded modern optics by presenting the earliest correct explanation of how human beings see. He was the first to set forth accurately what happens to light after it enters a telescope, and he designed a particular form of that instrument. His ideas provided a transition from the ancient geometrical description of the heavens to modern dynamical astronomy, into which he introduced the concept of physical force.
On December 27, 1571, in the German town of Weil der Stadt, then a "free city" within the Holy Roman Empire, Johannes was born prematurely, the offspring of an unhappy marriage. His father was a ne'er-do-well mercenary soldier, his mother the quarrelsome daughter of an innkeeper. Small in stature, Johannes never enjoyed robust health, but his superior intelligence was recognized even when he was a young child. Coming from a poor family, he would have received no education had not the dukes of Wrttemberg adopted the enlightened policy of providing generous scholarships for the bright sons of their impoverished subjects.
With such help Kepler in 1587 was able to attend the University of Tbingen, where he had the good fortune to study astronomy under Michael Mstlin, a professor who may have been unique in his day, for he was convinced that the astronomical system propounded by Nicolaus Copernicus was basically true: the Earth is a planet that rotates daily around its own axis and revolves annually around the Sun. Kepler's youthful acceptance of Copernican astronomy profoundly affected the subsequent course of his life.
After obtaining the B.A. in 1588 and the M.A. in 1591, Kepler planned to become a Lutheran minister. But in 1594, during his last year of training in theology at Tbingen, the teacher of mathematics in the Lutheran high school of Graz, in Austria, having died, Kepler was strongly recommended by the Tbingen faculty to fill the vacancy. Kepler did not finish the theology course at Tbingen but went to Graz the same year. On a summer day in 1595, while he was teaching a class, a spectacular idea flashed through his mind. Ancient Greek geometry had proved that there were five regular solids, or "Platonic bodies": tetrahedron (pyramid), cube, octahedron (formed by eight equilateral triangles), dodecahedron (12 pentagons), and icosahedron (20 equilateral triangles). The ancients knew that these five solids could be enclosed in a sphere, and that there can be no additional regular solids. Sustained by a vision of mathematical harmonies in the skies, a vision he derived from the philosophy of Plato and the mathematics of the Pythagoreans, Kepler tried to relate planetary orbits with geometrical figures.
According to Copernican astronomy there were six planets, whose orbits were regulated by the turning of invisible spheres. But why were there only six planets and not nine or 100? Was the cosmos so constructed that one of the five regular solids intervened between each pair of the unseen spheres, which carried the six Copernican planets? This nest of alternating planets and regular solids constituted the main theme in Kepler's Prodromus Dissertationum Mathematicarum Continens Mysterium Cosmographicum ("Cosmographic Mystery"), which he published in 1596 under the auspices of the Tbingen faculty. The Platonic and Pythagorean components in Kepler's conception of celestial harmony, however mystical in origin, helped to lead him to the three principles of planetary motion now known by his name.
Kepler sent copies of his first major work to a number of scientists, including Tycho Brahe, who was soon to become the imperial mathematician of the Holy Roman Empire. Although Brahe did not agree with the underlying Copernican foundation of Kepler's Mysterium Cosmographicum, he was so impressed by the author's knowledge of astronomy and skill in mathematics that in 1600 he invited him to join his research staff in the observatory at Benatek (now Bentky nad Jazerou), outside Prague. When Brahe died the next year, Kepler was promptly appointed his successor as imperial mathematician. His first publication at Prague, De Fundamentis Astrologiae Certioribus (1601; "The More Reliable Bases of Astrology"), rejected the superstitious view that the stars guide the lives of human beings. Nonetheless, his deep feeling for the harmony of the universe included a belief in the harmony between the universe and the individual, and his skill in astrological prediction was much in demand.
While Kepler was watching a rare conjunction of Mars, Jupiter, and Saturn in October 1604, a supernova appeared that remained visible for 17 months. This event was evidence that the realm of the fixed stars, considered since ancient times as pure and changeless, could indeed experience change. He published the results of his observations in 1606 as De Stella Nova in Pede Serpentarii ("The New Star in the Foot of the Serpent Bearer").
Kepler now had access to Brahe's incomparable collection of astronomical observations, the result of decades of unremitting and painstaking toil by the greatest naked-eye observer of the heavens and the leader of a highly qualified team of astronomers. As a member of the team, Kepler had been assigned to investigate the planet Mars. But, before he could use the raw observations, Kepler felt that he had to solve the problem of atmospheric refraction: how is a ray of light, coming from a distant heavenly body located in the less dense regions of outer space, deflected when it enters the denser atmosphere surrounding the Earth?
Kepler incorporated his results in a book that he modestly entitled Ad Vitellionem Paralipomena, Quibus Astronomiae Pars Optica Traditur, (1604; "Supplement to Witelo, Expounding the Optical Part of Astronomy"); Witelo (Latin Vitellio) had written the most important medieval treatise on optics. But Kepler did much more than add to his work. He made an analysis of the process of vision that provided the foundation for all of the advances in the understanding of the structure and function of the human eye. Kepler wrote that every point on a luminous body in the field of vision emits rays of light in all directions, but that only those rays can enter the eye that impinge on the pupil, which functions as a diaphragm. He stated that the rays emanating from a single luminous point form a cone, the circular base of which is in the pupil. All of the rays are then refracted within the normal eye to meet again at a single point on the retina, identified by Kepler as the sensitive receptor of the eye. If the eye is not normal, the second short interior cone comes to a point not on the retina but in front of it or behind it, causing blurred vision. For more than three centuries eyeglasses had helped older persons to see better. But nobody before Kepler was able to explain how these little pieces of curved glass had worked.
After the invention of the telescope had been reported to Galileo, who promptly proceeded to make his astounding discoveries, Kepler applied the same ideas concerning optics to the explanation of how the telescope works. Although Galileo's findings were received in general with skepticism and ridicule, Kepler acknowledged the Italian's accomplishments in his Dissertatio cum Nuncio Sidereo Nuper ad Mortales Misso a Galilaeo Galilaeo in 1610.
Galileo did not return the compliment. He chose to ignore the epoch-making results Kepler had published the preceding year. (See Kepler's theory of the solar system.) In his Astronomia Nova ("New Astronomy") of 1609, Kepler had demonstrated that the orbit of the planet Mars is an ellipse. Although it had been believed since antiquity that the planets, being heavenly bodies, were perfect and therefore could move only in perfect circles or combinations of circles, Copernicus had correctly classified the Earth as one of the planets; and it was fully accepted that the Earth was far removed from perfection. Kepler extended Copernicus' reasoning to the other planets and was the first to declare that the other planets resemble the Earth in being material bodies. That a material body, being imperfect, need not travel in a perfectly circular orbit was a conclusion made by Kepler after he tried unsuccessfully to fit the orbit of Mars to Brahe's observations in every possible combination of circles his ingenuity could devise. Because none of them worked, he tried noncircular paths until he found the true solution: Mars revolves in an elliptical orbit with the Sun occupying one of its two focuses.
The pre-Keplerian dogma that permitted only circular paths entailed the concept of uniform motion--i.e., the moving body or point must traverse equal arcs in equal intervals of time. Such a conception of uniform motion as measured along an arc was, of course, incompatible with an elliptical orbit. But Kepler found an alternative form of uniformity. This new uniformity equated equal areas with equal times. With the Sun remaining stationary in one focus of the ellipse, the planet, while revolving along the periphery of its elliptical orbit, would sweep out, in equal intervals of time, equal areas of the ellipse, not equal arcs along the periphery of the ellipse.
In 1619, 10 years after Kepler published these first two principles of planetary motion (the elliptical orbit and equality of areas), he published the Harmonice Mundi (Harmonics of the World), in which he expounded his third principle, which related a planet's mean distance from the Sun to the time it takes to complete its elliptical orbit around the Sun. The cube of the distance proved to be in a constant ratio to the square of the time required for all the planets to complete such an orbit. The enunciation of this rule (which is sometimes called the 3/2 ratio) completed Kepler's contribution to the understanding of planetary motion and helped to prepare the way for Sir Isaac Newton's exposition of universal gravitation, which affects all of the material bodies in the physical universe.
Meanwhile, Kepler's patron, the Holy Roman Emperor, had been compelled by his brother to abdicate, and Kepler himself had found it desirable to leave Prague, then the capital of the empire. Although he was reappointed imperial mathematician by the new emperor, Kepler moved to Linz, in Austria. His first wife had died in Prague; Kepler remarried in 1613. Once, when buying supplies for his new home, Kepler became unhappy about the rough-and-ready methods used by the merchants to estimate the liquid contents of a wine barrel. Because the curved containers they used were of various shapes, Kepler sought a mathematical method for determining their volumes. Following the model established by Archimedes, the most talented mathematician of antiquity, Kepler, in his volumetric researches, investigated the properties of nearly 100 solids of revolution--made by rotating a two-dimensional surface on one of its axes--that had not been considered by Archimedes. Starting with an ordinary wine barrel, Kepler enormously extended the range of Archimedes' results. He did so by refusing to confine himself, as Archimedes had done, to cases in which a surface is generated by a conic section--a curve formed by the intersection of a plane and a cone--rotating about its principal axis. Kepler's additional solids are generated by rotation about lines in the plane of the conic section other than its principal axis.
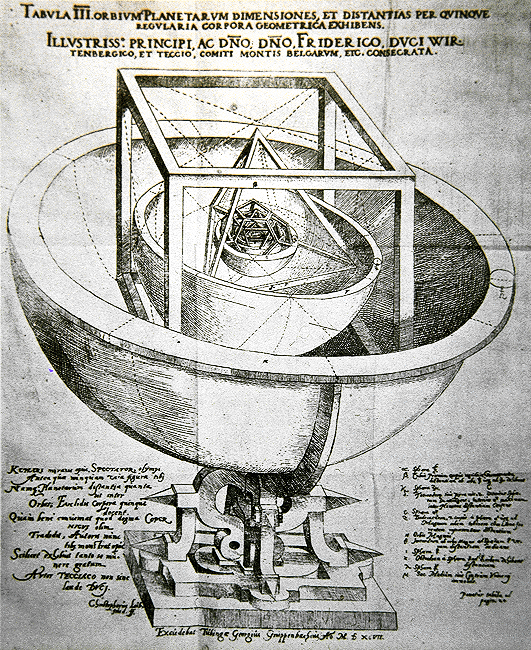
While he was in Linz, Kepler published his Epitome Astronomiae Copernicanae (1618-21; Epitome of Copernican Astronomy). He modelled this title after the highly successful introduction to astronomy that had been published by his former Tbingen professor in a number of editions. But, whereas Mstlin had deemed it prudent pedagogical practice to keep Copernicanism out of an elementary textbook, which he therefore entitled simply "Epitome of Astronomy," Kepler emphasized his open espousal of the new cosmology by inserting the provocative label "Copernican."
In Linz in 1620, Kepler heard that his mother had been indicted on the charge of being a witch. Such a defendant was often subjected to torture and, if convicted, was usually burned at the stake. If his mother had suffered this fate, Kepler's own status as imperial mathematician of the Holy Roman Empire and mathematician of Upper Austria might have been irreparably impaired. He rushed to her defense, therefore, not only out of filial devotion but also out of prudent self-interest. Only his skillful intervention saved her from torture and a fiery death.
Kepler had planned to publish his Tabulae Rudolphinae (Rudolphine Tables), named in honour of his first imperial patron, Rudolph II, in Linz. But this work, the final outcome of long years of unceasing reflection and tireless calculation, could not be printed there because of a rebellion by the peasants, who were infuriated by a combination of being forced to return to Catholicism and to pay heavy taxes. Kepler had to find another home and a new patron.
Albrecht von Wallenstein, duke of Friedland and Zagan, a successful soldier of fortune who had put his private army at the disposal of the empire in the Thirty Years' War, accepted the responsibility of satisfying Kepler's financial needs. The astronomer moved to Zagan in Silesia, where he was able to establish his own printing press. The Rudolphine Tables were printed at Ulm, Germany, in 1627, before Kepler went to Zagan in 1628. But Wallenstein turned out to be someone on whom Kepler could not rely.
Leaving his family behind in Zagan, Kepler went west to collect the interest due on two promissory notes he held in exchange for money he had deposited in Austria. On his way he stopped at Regensburg, where the Imperial Diet was in session. He fell acutely ill and died on November 15, 1630. The tremendous upheavals suffered by Germany in the Thirty Years' War later obliterated his grave.
Excerpt from the Encyclopedia Britannica without permission.