What Was Llull Up To?
Anthony Bonner
Annibal, 25, 7
07013 Palma de Mallorca
In the histories of logic and of computer science which mention precursors and pioneers, we often find mention of Leibniz, the great l7th-century mathematician and philosopher, who was one of the first to try to build a mechanical calculator, and who tried to formulate a Mathesis universalis, a sort of scientific language which would permit any two disputants to settle their differences merely by taking pencil and paper and saying, "Let us calculate" But then we find that Leibniz got certain important ideas from a character called Ramon Llull who lived in the l3th century, who carne from a place called Mallorca, and who spent his life trying to convert Muslims and Jews. As if this weren't peculiar enough, when he has appeared in modern treatises, it has usually been as the typical romantic genius or in his case, medieval mystic who wasn't quite right in the head. Even a man as sensible as Martin Gardner (1982) calls him quixotic and paranoid!. So what Llull was up to is a question that indeed needs a bit of clarification.
Perhaps the best way to begin is by trying to situate him in his time. He was born here on Majorca around 1232, only two or three years after the King of Aragon and Catalonia had recovered the island from the Muslims. This meant that Llull grew up in an island that was still strongly multicultural: Muslims continued to represent perhaps a third of the population, and Jews, although a much smaller minority, were an important economic and cultural force on the island. So when at the age of thirty he was converted from a profligate youth and he decided to devote his life to the service of the Church, it seemed only logical to do so by trying to convert these "infidels", as they were then called. And he decided to do this in three ways: (1) to develop a system that his adversaries would find difficult to refute (which is what we'll see in moment), and to try to persuade them of the truth of Christianity instead of just trying to refute their own doctrines, as his predecessors had done (1); (2) to be willing to risk his life in proselytizing among Muslims and Jews (he in fact made three trips to North Africa); and (3) to try to persuade Kings and Popes of the need for setting up language schools for missionaries, for which purpose he traveled many times throughout France and Italy. He lived to 83 or 84, an incredible age when the average life-span was around 40, dying in 1316 (2).
Now this situation has presented historians with two serious paradoxes. The first is that, if he was principally interested in converting Muslims and Jews, what could this possibly have to do with his being a pioneer of computer science? It would seem doubtful that l3th-century unbelievers would have wanted to listen to arguments that looked forward to Bill Gates, or that modern computer scientists would deem their profession useful for the persuasion of Muslims and Jews of the truths of Christianity. The second paradox is that the system Llull thought up doesn 't look like anything his contemporaries were using, nor can it be considered really acceptable to modern logic. This second paradox has caused enormous problems for historians of logic. Those equipped with a knowledge of medieval logic who try to tackle Llull are disagreeably surprised to find him discussing either not at all or passing over very superficially the topics they feel he should be discussing, and which they know his contemporaries were discussing. Those who try to tackle it from the point of view of modern formal logic are understandably put off by his basing his system on an extreme Platonic realism, and thus making it depend primarily on meaning rather than form. Llull himself was aware of these problems, and carefully tried to explain that his system was neither logic nor metaphysics. But that only helps us to understand what it isn't; what it is is something I will try in very broad outline to explain now. But before doing so, I would ask you to suspend, for the moment at least, your highly trained and normally indispensable sense of disbelief, and only start applying it again when we've seen a bit of the inside of the edifice Llull constructed, because if not, we'll never get past the front door.
The first thing we have to face is the problem of his trying to persuade unbelievers. From the outset Llull realized that previous attempts had failed because people had based their arguments on sacred texts. Christians argued positively trying to explain the truths of the Bible, or negatively trying to point out the errors in the Qu'ran or in the Talmud. Such discussions, however, invariably became bogged down in arguments as to which texts were acceptable to whom, and how to interpret them. Since it was clearly impossible for opposing sides to agree on these points, such discussions never got anywhere. Participants invariably left them with a feeling of having tried unsuccessfully to walk uphill in sand.
So Llull decided to try something completely abstracted from the specific beliefs of any one religion, based only on whatever beliefs or areas of knowledge they had in common. All three religions, for instance, were monotheistic, and none of them could deny that this one God of theirs had a series of positive attributes: goodness, greatness, eternity, etc. They also shared a common heritage of Greek science which taught them about the earth at the center of a universe with seven planets rotating around it, and that this earth of ours was composed of four elements, fire, earth, air and water. And the framework in which all three philosophized about the world was that of Aristotle. Finally, all could agree more or less about what constituted virtues and vices.
What Llull then set out to do was to show how one could combine these theological, scientific and moral components to produce arguments that at least couldn't be rejected outright by his opponents. It was furthermore clear that if he was going to set up an Ars combinatoria, as later generations called it, its components would have to be finite in number and clearly defined. Since they were like the premises of his arguments, everybody had to be quite clear as to what they were and how they functioned. Saying that people retained visual images better than words, he decided to present his system graphically. This he did in two stages: the first version of his system had twelve or more figures, and he finally had to jettison it in the face of contemporary complaints about its being too complicated (3). The second version in which the figures were reduced to four is the one for which he was chiefly known in the l6th and l7th centuries, and which we will present here. The final version of this second system found expression in two works: the "Ars generalis ultima" (4), along with a much shortened introductory version of same, the Ars brevis (5), which follows the longer one chapter by chapter, but in outline form.
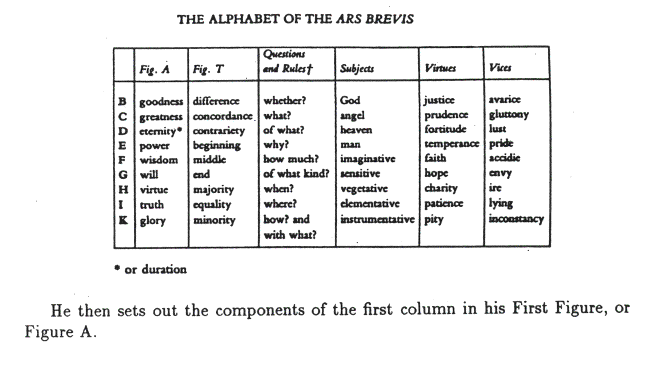
These works begin with an "Alphabet" giving the meaning of nine letters, in which he says, "B signifies goodness, difference, whether?, God, justice, and avarice. C signifies...", and so on, all of which can best be set out in a table (6).

Notice first of all, as always with Llull, the letters don't represent variables, but constants. Here they're connected by lines to show that in the Divinity these attributes are mutually convertible. That is to say that God's goodness is great, God's greatness is good, etc. This, in turn was one of Llull's definitions of God, because in the created world, as we all know too well, people's goodness is not always great, nor their greatness particularly good, etc. Now such a system of vertices connected by lines is what, as mathematicians, you will of course recognize as a graph. This might seem to be of purely anecdotal interest, but as we shall see in a moment, the relational nature of Llull's system is fundamental to his idea of an Ars combinatoria.
The components of the second column are set out in a Second Figure, or Figure T (7)
Here we have a series of relational principles related among themselves in three groups of three, hence the triangular graphs. The first triangle has difference, concordance, and contrariety; the second beginning, middle, and end; and the third majority, equality, and minority. The concentric circles between the triangles and the outer letters show the areas in which these relations can be applied. For example, with the concept of difference, notice how it can be applied to sensual and sensual, sensual and intellectual, etc. "Sensual" here means perceivable by the senses, and Llull explains in the Ars brevis, that: "There is a difference between sensual and sensual, as for instance between a stone and a tree. There is also a difference between the sensual and the intellectual, as for instance between body and soul. And there is furthermore a difference between intellectual and intellectual, as between soul and God".

Here Llull explains that B C, for instance, implies four concepts: goodness and greatness (from Figure A), and difference and concordance (from Figure T), permitting us to analyze a phrase such as "Goodness has great difference and concordance" in terms of its applicability in the areas of sensual/sensual, sensual/intellectual, and intellectual/intellectual. It furthermore, as he points out, permits us to do this systematically throughout the entire alphabet. This is important, because one of the ways in which Llull conceived his Art as "general" was precisely in its capacity to explore all the possible combinations of its components.
Now as mathematicians, you will recognize this figure as a half matrix, and you will also see that, in relation to the graph of the First Figure, it is an adjacency matrix. Because such a matrix is symmetrical (in Llull's case this means he makes no distinction between B-C and C-B), he saw no reason to reproduce the other half; and because his graph admits no loops (that is, omits relations such as B-B), he could also omit the principal diagonal.
If the Third Figure explores all possible binary combinations, the Fourth Figure does the same for ternary combinations.
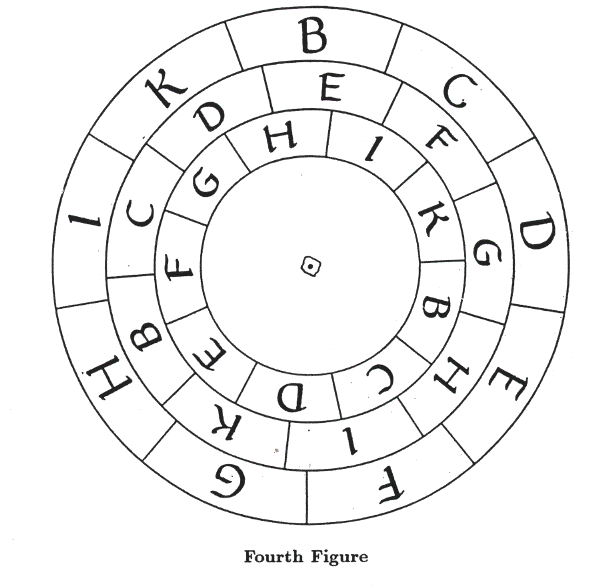
In medieval manuscripts, the outside circle is normally drawn on the page, and the two inner ones are separate pieces of parchment or paper held in place on top of it by a little piece of string, permitting them to rotate in relation to each other and to the larger circle. In a moment we'll see how he uses these ternary relations, but before going on let me quote a book on logic for computer applications (Nerode and Shore, 1993). Its authors say that one of the things lacking in classical Aristotelian logic was the notion of a relation with many arguments. His predicate relations P(x) were unary, and what he missed was the basic building-block character of binary relations R(x1y) and ternary relations S(x,y,z). This shows that imbedded in what Künzel and Cornelius (1991) have called the "hardware" of Llull's system we already have a full panoply of binary and ternary relations.
Binary relations are worked out more extensively in a section he calls "The Evacuation of the Third Figure". For the "compartment", as he calls it, of B C, he not only uses "goodness" and "greatness" from the First Figure, and "difference" and "concordance" from the Second Figure, but also the first two questions of the third column of the alphabet, those also corresponding to the letters B C, which are "whether?" and "what?" This means that for the combination of "goodness" and "greatness" one has three possibilities, a statement and two questions:
- Goodness is great.
- Whether goodness is great.
- What is great goodness?
and so on for "goodness" and "difference", "goodness" and "concordance", for a total of 12 propositions and 24 questions.
Ternary relations are worked out in a Table based on the Fourth Figure:

The one we show here is the shortened form from the Ars brevis; instead of 7 columns, the full form of the Ars generalis ultima has 84! Here the letter T acts as a separator: the letters that precede it in any one compartment are from Figure A whereas those that follow it are from Figure T. In addition the first letter can act as an indicator of what question from the third column of the alphabet should be considered. So, for instance, the ninth entry of the first column, B T B D, could be translated as "Whether goodness contains in itself difference and contrariety".
So much for the bare mechanics of the Art. Beyond that Llull wanders even farther from the path of modern logic by basing his Art not on the form of his propositions, but on the meaning of their premises. It is therefore much more intensional than extensional. How this side of his Art functions can perhaps best be explained by making a brief excursion into Lullian definitions, and into the questions and rules.
Now these definitions of his were based on how he felt the world functioned. He proposed, in fact, a vision of reality which was as novel as the system he built. He said that nothing whatever (and of course for him, much less God) was inactive. Nothing just sat there being itself; it also did whatever its nature called upon it to do. He often used the analogy of fire which wasn't only a thing in itself, but also was active in the production of heat. So also was goodness not only a thing in itself, as, for instance, an essential attribute of God, but it also produced goodness, and this in two ways: interiorly making His greatness, etc. good, and exteriorly creating the world's goodness (or lack of it where evil was concerned). Here again he frequently used the analogy of fire, which in itself creates a flame and heat, and exteriorly, as he said, causes the water in a pot to boil. Moreover, anything active has to have a point of departure (in the case of the thing that produces good, he called it "bonificative"), an object which it affects (the "bonifiable"), and the act itself going from one to the other (that is, which "bonifies"). And it wasn't only God's attributes that were active in this way; every rung of the scale of being was similarly articulated with the three correlatives (as he called them) of action. At the bottom of the ladder, fire had its "ignificative", "ignifiable", and "ignifies", and in the middle, the human mind had "intellective", "intelligible" or "understandible", and "understanding". The world was thus for him a vast dynamic web of ternary relations working both individually or interiorly, as I said before, and exteriorly one upon the other. It was this web of relations that was implied by his definitions. For example, "goodness" the first component of Figure A, he defined interiorly as "that thing by reason of which good does good". But notice how the exterior definition of the second component, "greatness", as "that by reason of which goodness, duration, etc. are great", implies that even goodness could also be defined similarly in terms of the other components of Figure A. So these definitions, which to some commentators have seemed simply tautological, in fact imply a dynamic reality articulated in a large web of interrelations.
Now this definitional doctrine turns up under one of the questions of the third column of the Alphabet of the Art. Not under the first question of "whether?" which inquires into the possibility of a thing existing, but under the second which asks "what" a thing is. This question (or rule, as Llull also calls it) is divided into four species. In the Ars brevis Llull uses the example of the intellect instead of goodness to illustrate how it works, saying that "The first [species] is definitional, as when one asks, What is the intellect? To which one must reply that it is that power whose function it is to understand". Notice how this is identical with that of "goodness" as being "that thing by reason of which good does good". The second species goes further and asks, "What does the intellect have coessentially in itself? To which one must reply that it has its correlatives, that is to say, intellective, intelligible, and understanding, without which it could not exist, and would, moreover, be idle and lack nature, purpose, and repose". This refers, of course, to the ternary dynamic structure we already mentioned. We're also by now familiar with the third species, which is when one asks, "What is the intellect in something other than itself? To which one must reply that it is good when understanding in goodness, great when understanding in greatness, etc.". Here we are with the equivalent of "greatness" as being "that by reason of which goodness, duration, etc. are great" which we saw before. The rest of the questions and rules continue in the same vein, carefully distinguishing the different ways in which one can formulate questions such as "of what?" which inquires about material qualities, "why?" which asks about formal causes, "how much?" concerning quantity, "of what kind?" concerning quality, and so oil.
So when Llull starts combining elements of the first two figures to answer questions or make proofs, he carefully shores up his arguments with the appropriate definitions and rules. 1 won't show you how this works in practice, because it would involve delving into too many minutiae of his explanations. I would just like to make a few general remarks. The first to answer a doubt that has probably occurred to you: how can Llull prove anything useful if, as I said before, he limits himself to such divine attributes such as goodness, greatness, etc., which seem hopelessly vague and general in nature? The answer is that in the first place he occasionally lets one see how definitions can be more widely applicable than they might seem. In the above definition of the intellect; for instance, when he says "it is good when understanding in goodness, great when understanding in greatness, etc.", he adds "and [it is] grammatical in grammar, logical in logic, rhetorical in rhetoric, etc.", so right away we are applying these concepts to other fields. Secondly, notice how in the Alphabet, the fourth column of "Subjects" is a ladder of being in which "everything that exists is implied, and there is nothing that exists outside it", as Llull says in the Ars generalis ultima (IX, 1). The ninth chapter of that work offers a detailed study of each rung in terms of the 18 principles of Figures A and T, and in terms of the 9 rules. The last rung of Instrumentative includes the moral instruments of the virtues and vices which appear in the last two columns of the alphabet, and which, in his more popular works, Llull uses as important tools of persuasion. In yet another adventure into outside material, Llull presents a chapter on "Application" which gives definitions of what he calls the "Hundred Forms" to which the mechanisms of the Art can also be applied. Here he includes every subject imaginable: physical, conceptual, geometrical, cosmological, social, etc. Lest you think we're still operating in a sort of misty area of vague generalities, let me offer the counter-example of Form no. 96 on Navegation in the Ars generalis ultima, which in fact consists of a little five-page manual with worked examples of how to find your position at sea!
Your chief objection that this continual reference to the real world (in the Platonic sense that Llull understood it) on which the Art is firmly based, places it at an opposite pole from any kind of formal logic is undeniable. As I said before, however, Llull was aware of this point, and was at pains to make clear that his Art was neither logic nor metaphysics. My feeling, however, is that the Platonic basis of his system is not without historical or conceptual interest; we must remember Leibniz's comment that if someone could reduce Plato's thought to a system, he would render humanity a great service (8). Secondly, Llull's invention of an ars combinatoria as the only possible way of dealing with interrelationships of Platonic forms, was to have a considerable impact in the Renaissance, and would, as my colleague Ton Sales will explain, have a decisive influence on Leibniz.
In one sense, however, Llull's system was more abstract and more amenable to analysis by modern mathematical methods. This was in his attempt to systemize not only totally but even semi-mechanically its all-embracing relational nature. This is, of course, what we mean when we say that he developed an ars combinatoria. His use of graphs, along with their alternate representation as matrices, to display the relational structure of his system shows a certain understanding of the general nature of the problem. But there is another aspect of his system which also has curious modern parallels.
The first period of the Art, which we haven't touched on today, very frequently developed its arguments or proofs by pairwise comparison of concepts. Let me briefly show one such proof from a central work of that period, the Ars demonstrativa. Here he always starts his proofs with a series of concepts within what he calls a compartment (or camera), as you can see in the figure.
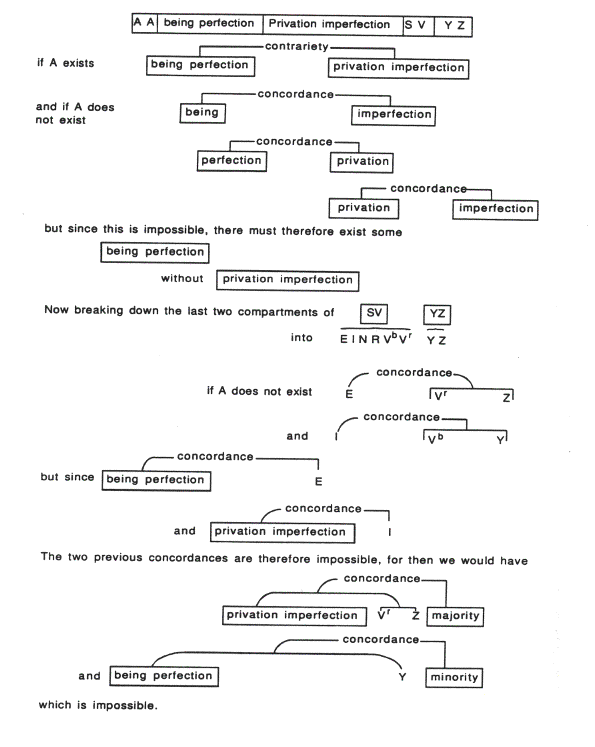
The four words not presented by letter symbols come from a Figure X, which disappeared from the later version of the Art, and as you can see, they represent opposites, "privation" being a synonym of "non-being". Notice also the words "contrariety" and "concordance" written above the compartments, which you will recognize as coming from Figure T.
Now A stands for God, and it is double because he is exploring two hypotheses, a positive and negative. The positive one presents no problem: if God exists, there exists a perfect being contrary to privation (or non-being) and imperfection. If, however, God does not exist, then all being has some imperfection, and the only thing that's perfect is non-being or privation, which of course accords with imperfection. Since the concordance of perfection and imperfection is clearly contradictory, the existence of God has been proved by reductio ad impossibile. I won't explain the second half of the proof, except to say that it functions similarly.
As you can see the technique of beginning with a hypothesis and working down a branching structure to a confirmation or refutation, bears a certain resemblance to the tableaux methods of Gentzen, Beth and Smullyan. Notice furthermore how it works by a series of pairwise comparisons.
Which brings me to a further curious piece of evidence recently brought to light by two English scholars. In the social sciences, the modern deductive theory of voting was initiated in the 1950's by Arrow (1951) and Black (1958), with techniques of paired comparisons which in graph theory are called "tournaments". Now the usual history of voting theory says that they were preceded by two Frenchmen, Borda and Condorcet in the l8th century, whose discoveries were forgotten and repeated from scratch by Lewis Carroll, whose work was again utterly neglected. What Mclean & London (1990 & 1992) have shown is that Condorcet and Borda were preceded by half a millenium by Ramon Llull, "who made one of the first systematic contributions to the deductive theory of voting", and this with slightly varying systems presented in two different works. One is aptly called the Ars electionis, but the other one is, of all things, embedded in the novel Blaquerna, where Llull uses it to explain how nuns should elect their abbess!
What's significant about this, it seems to me, is not so much Llull as the neglected genius, but rather as a thinker with enough breadth of vision to see in his discoveries a generality greater than the initial uses for which they were intended. To a professional mathematician of the late 20th century the connections between "tournaments", graph theory and combinatorics is obvious, but that a l3th-century Majorcan missionary should have seen the connection is, I think interesting.
I would like to end on a more personal note, or what in the scientific community could fall under the euphemistic heading of a call for papers. On the negative side, we have shown that Lull's Art was not a formal logic, but the positive side is unusual and still in many ways in need of explanation. It was highly structured system, to the point of being semi-mechanical. And the more one deals with it, the more consistent and interesting it seems to become. Lastly, its structure was relational and combinatorial, thus mirroring a world which Llull saw as primarily relational. Might these factors not make it possible to program at least part of the Art in a relational language such as Prolog? And if so, might this not clarify to us, that is, by putting it into modern terms the functioning of this lath-century computer? The basic problem, as I see it, is that here we have inherited an ancient computer made of parchment and ink, but along the way the manual got lost. We have many of the materials to make a new one, and if you ask, well, what use would it be, I would answer what a professor from New York University answered some years ago. He was an arachnologist, and when a reporter asked him what good spiders were, he replied, "Spiders are damned interesting, that's what good spiders are".
Abbreviations
MOG = Raymundi LuIli Opera omnia, Ivo Salzinger editor, 8 vols., Mainz, 1721-1742 (reprintFrankfurt, 1965)
ROL = Raimundi Lulli Opera Latina, F. Stegmüller et al., editors, 21 vols. published so far, Palma de Mallorca/Turnhout, Belgium, 1959.
References
1. Beth, E. W. (1962) Formal Methods; An introduction to symbolic logic and to the study of effective operations in arithmetic and logic, D. Reidel, Dordrecht.
2. Bonner, A. (1994) "Ramon Llull: relació, acció, combinatòria i lògica moderna", Studia Lulliana 34, pp. 51-74.
3. Colomer, E. (1979a) "Ramon Llull, ┐precursor de la informática?", Boletín CITEMA 81, pp. 7-44.
4. Colomer, E. (1979b) "De Ramon Llull a la moderna informática", Estudios Lulianos 23, pp. 113-135.
5. Deo, N.,
(1974) Graph Theory, with Applications to Engineering and Computer Science, Prentice-Hall, Englewood Cliffs, N.J.6. Fleckenstein, J. O. (1967) "Leibniz's algorithmic interpretation of Lullus' art", Organon (1nstitut d'Histoire de la science et de la technique aupres de l'Académie Polonaise des Sciences) 4,171-180.
7. Foulds, L.R.
(1992) Graph Theory Applications, Springer-Verlag, New York/Berlin.8. Gardner, M. (1982) "The Ars Magna of Ramon Lull", Logic Machines and Diagrams, University of Chicago Press, Chicago.
9. Gentzen, G. (1969) The Collected Papers of Gerhard Gentzen, North-Holland, Amsterdam.
10.
Künzel W. and Cornelius, H. (1991) Die Ars Generalis Ultima des Raymundus Lullus. Studien zu einem geheimen Ursprung der Computertheorie, Berlin.11.
Llull, R. (1978) Ars notatoria, J. Gayà' editor, CITEMA, Madrid.12. Llull, R. (1985) Selected Works of Ramon Llull (1232-1316), A. Bonner, editor, 2 vols. Princeton University Press, Princeton, N.J.
13. Llull, R. (1993) Doctor Illuminatus. A Ramon Llull Reader, A. Bonner and E. Bonner, editors, Princeton University Press, Princeton, N.J.
14.
McLean, I. and London, J. (1990) "The Borda and Condorcet Principles: Three Medieval Applications", Social Choice and Welfare 7, 99-108.15. McLean, 1. i London, J. (1992) "Ramon Llull and the Theory of Voting", Studia Lulliana 32, 21-37.
16. Maróstica, A. H. (1992) "Ars combinatoria and Time: Llull, Leibniz and Peirce", Studia Lulliana
32, 105-134.17. Nerode, A. and Shore, R. A.
(1993) Logic for Applications, Springer Verlag, New York/Berlin.18.
Orio, B. (1994) "Leibniz y la tradición neoplatónica. Estado actual de la cuestión╗, Revista de Filosofía 7 , p. 493-517.19.
Smullyan, R. M. (1968) First Order Logic, Springer-Verlag, Berlin.
1. The tactic was psychologically important. Instead of forcing his adversaries to justify their own faith, he gave them the opportunity to "falsify", as Popper would say, Christianity.
And not dying martyred, as pious legends would have it. He is buried in Palma, in the Church of San Francisco.3. This first version of the Art (of which we'll get a glimpse at the end of this paper)
was logically quite different from the second, and included two iuteresting attempts to establish a new notation, one in the Ars notatoria (see Llull, 1978), and the other in the Introductoria Artis demonstrativae printed in MOG III.4. The best edition is that of ROL XIV.
5. The Latin text is in ROL XII, and an English translation in Llull (1985) and (1993).
6. The reader mustn't be disturbed by the lack of the letter J, which didn't exist as a separate letter in Llull's time. The Middle Ages used I/J as well as U/V interchange
ably; they weren't differentiated till the Renaissance. It received the letter T because in the previous version of the Art the alphabet used not just nine but all the letters of the alphabet, and the position of this figure followed that of a Figure S. Even though the intervening letters aud figures disappeared from his system, Llull, perhaps not to confuse users of the earlier system adapting to his "update", continued referring to as Figure T. Quoted in Orio (1994).