THE BEGINNINGS OF ALGEBRAIC THOUGHT IN
THE SEVENTEENTH CENTURY¹

The explanation for this tension may well lie in the fact that both mathematicians treated old problems by means of a new symbolic algebra, without themselves being clear on the extent to which the new means had changed not only the techniques of solution but also the very manner of posing problems. With the new algebra, the ars analytica, mathematicians thought at first that they had regained the mathematics of the Golden Age of antiquity.⁵ Within a short time, however, the highest achievements of Greek mathematics had been exceeded, and it gradually became clear that something brand new was at hand, something of which the scope was almost limitless.⁶ In the meantime, mathematicians were subject to the tension mentioned above.

In the light of the brilliant mathematical achievements of the later seventeenth century , in particular the infinitesimal calculus, there is a risk of overlooking the most important and basic achievement of mathematics at the time, to wit, the transition from the geometric mode of thought to the algebraic. In what follows, we shall investigate this transition somewhat more closely, and we shall do so in two ways. First, we shall analyse the algebraic mode of thought conceptually and offer some examples to document its presence in the early seventeenth century .Then we shall show how the transition to this mode of thought cannot be explained solely by the internal developmental tendencies or needs of mathematics at the time; rather, to understand the transition correctly and to judge its historical importance, the historian must include in his consideration developments in other intellectual areas.

First, then, what should be understood as the "algebraic mode of thought"? It has three main characteristics: first, this mode of thought is characterized by the use of an operative symbolism, that is, a symbolism that not only abbreviates words but represents the workings of the combinatory operations, or, in other words, a symbolism with which one operates.⁷ Second, precisely because of the central role of combinatory operations, the algebraic mode of thought deals with mathematical relations rather than objects. Even when certain relations become themselves objects, say the set of group morphisms, one seeks the relations that link these new objects.⁸ The subject of modern algebra is the structures defined by relations, and thereby one may note as a corollary that the algebraic mode of thought rests more on a logic of relations than on a logic of predicates. Third, the algebraic mode of thought is free of ontological commitment. Existence depends on consistent definition within a given axiom system, and mutually compatible mathematical structures live in peaceful co-existence within mathematics as a whole. In particular, this mode of thought is free of the intuitive ontology of the physical world.⁹ Concepts like "space", "dimension", and even "number" are understood in a purely mathematical sense, without reference to their physical interpretation. In this respect, the algebraic mode of thought can be characterized as an abstract mode of thought, in contrast to an intuitive one.

The characteristics of Greek mathematics are almost diametrically opposed to those just cited. Greek mathematics almost completely lacked any symbolism, much less an operative symbolism. Even in the works of Diophantus one finds only a series of abbreviations for the purpose of saving words.¹⁰ Paul Tannery once noted that the Greek mathematicians lacked less the methods than the suitable formulas for describing the methods.¹¹ He was probably right regarding the lack of a symbolism. But many methods depend on the symbolism with which they are expressed, as the seventeenth century shows.¹²

The chief task of Greek mathematics was to discover the inherent properties of various geometric figures or of numbers as definite collections of units. Only in the analytic reduction procedures by which an unsolved problem is reduced to a solved one¹³ do we find any trace of a relational mathematics, or perhaps also in the first steps toward projective geometry in Pappus. That relations stood wholly in the back of the Greek mind is clear enough from the fact that Aristotle"s Organon contains no logic of relations.¹⁴ Finally, Greek mathematics was intuitional and strongly dependent on physical ontology.¹⁵ We need only point to the impossibility of multiplying more than three lines together (the product of two lines was conceived as a plane area, the product of three lines as a solid, and there were only three spatial dimensions), or to the classification of curves according to the possibility of their construction by means of straight-edge and compasses (Descartes¹⁶ was the first to note explicitly that straight-edge and compasses were, after all, also mechanical means of construction). Also, the concept of number as the thing counted, that is, as a collection of counted units, derived from this basically physical ontology of Greek mathematics.

If, then, the efflorescence of European mathematics in the sixteenth and seventeenth centuries is largely due to the reintroduction of the classical texts, we must nevertheless note that this heritage included a mathematical mode of thought diametrically opposed to the algebraic. What became of this heritage? We find in the seventeenth century an algebra of quantities that has a true operative symbolism. We find a theory of equations which is based on the conception of an equation as a relation among quantities and which serves the purpose of clarifying relations between equations and their solutions or between the solutions of one equation and those of others. That is, the structure of algebraic equations is being examined and with it such questions as those of solvability are being handled mathematically for the first time. We find a loosening, albeit incomplete, of mathematics from physical ontology. Clearly visible are a new concept of number and the overcoming of the dimensional limits of Greek intuition. In short, we find the first foundations of the algebraic mode of thought. Some examples may make this clearer.

In 1591 in his Introduction to the Analytic Art, the mathematician François Viète introduced a then brand new algebraic symbolism. In order that the setting up of equations:

...be helped by some art, it is necessary that the given magnitudes be distinguished from the uncertain ones being sought by a constant, perpetual, and highly conspicuous convention, such as by designating the magnitudes being sought by the letter A or some other vowel, E, I, O, U, Y; and the given magnitudes by the letters B, G, D, or other consonants.¹⁷

Viète, however, understood something else by "unknown". True, following Diophantus he calls it a species, and he calls algebra logistice speciosa; but he also says that this "logistic of species" shall be carried out using the "species or forms of things".²⁰ The form of the things denoted by alphabetical letters is purely and simply quantity: not just numbers or line segments, but everything for which it makes sense to say that it is added, subtracted, multiplied, and divided (think here of van Roomen's forty-fifth-degree equation that expresses the problem of dividing an angle into forty-five equal parts). Viète is raising algebra from a refined auxiliary technique for solving arithmetical problems to the language of mathematics itself.

Thereby, Viète is already pointing past the magnitudes themselves to the computational operations and to the ever more complicated expressions that can be formed by means of these computational operations. He is less concerned with the interpretation of the expressions than with their structure. More precisely, he is interested in the structure of the equation that results from setting two algebraic expressions equal to one another. For example, what is the relation between the roots of a given form of equation-because of the symbolic differentiation between unknowns and parameters, he can now study forms of equations instead of individual equations-and the parameters of that form of equation? With Viète's algebra, an essentially new task of the mathematician comes to the fore: the investigation of the constitutio aequationum, the structure of equations. Thereby, Viète becomes the founder of the theory of equations, one of the greatest achievements of the seventeenth century, if not the greatest of all.

The themes of Viète's algebra just mentioned find even clearer expression in the work of Descartes. Although Descartes insisted several times that he had read Viète's Introduction only after the publication of his own Geometry,²¹hemay still be viewed as having developed Viète's new ideas farther. With regard to symbolism, he differed at first from Vi6te only in that, instead of capital letters, he employed the small letters x, y, x for the unknowns and a, b, c for the parameters (as Fermat often noted, an arbitrary convention). But Descartes then went a step farther. He replaced the last vestiges of a verbal algebra with a particularly revealing symbolism. Instead of writing 2 A cubus, he wrote 2x³, for which he gave the following justification:²²x and x³ are quantities linked to one another and ultimately to a unit by means of certain relations, that is l:x = x:x² = x²:x³. Three relations lead from 1 to x³, and the number of these relations is given by the upper index number. It is here characteristic for a new mode of thought that Descartes does not say something like, x³ represents a cube constructed on side x, but that he considers this quantity simply as a quantity and connects it with a unit according to its structure. He goes even farther.

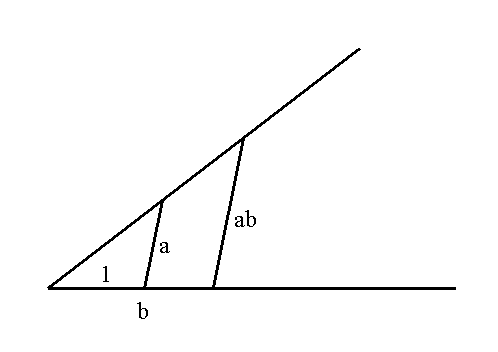
The very first problem in the Geometry, published in 1637, is that of justifying the application of algebra to geometry. It is treated in the first three pages of the work23 and shows clearly the new mode of thought under discussion here. Descartes wants to construct an algebra of line segments and must therefore show that the six basic operations of algebra (he counts raising to a power and taking a root, as well as addition, subtraction, multiplication and division), which in the realm of numerical algebra correspond to the arithmetical operations, have a geometrical interpretation. One can, of course, add any number of line segments, and a smaller segment can always be subtracted from a greater. But how does one multiply two line segments together? Initially, there is the classical procedure, by which one constructs a rectangle; a process, by the way, that Viète and (until about 1630) Descartes himself used. But a rectangle is not a line segment, and one seeks an algebra of line segments. Descartes' answer to this old problem of the dimensionality of the computational operations is dazzlingly simple; it follows from the concept of powers mentioned above. Assume a unit line segment, to which all other line segments are referred; if it is not given explicitly by the problem at hand, it may be chosen arbitrarily.24 To multiply two line segments a and b, one then needs only construct a triangle, of which one side is a and the other side is the unit segment. In a similar triangle, of which the side corresponding to 1 is b, the other side, corresponding to a, will be ab. By means of the proportion 1:a = b:ab, one sees immediately that ab contains two relations to the unit length. Put anachronistically - how anachronistically remains to be seen - Descartes shows that the line segments (with multiplicative unit) form an algebraic field. One is tempted to say that mathematics is already on the way toward the investigation of algebraic structures.

The title of the Geometry is deceptive, for the work is in large part a treatise on algebra. The third book, which constitutes more than a third of the whole, contains a purely algebraic theory of equations. It is designed to make it possible for the mathematician to analyse the structure of a problem, whatever the particular quantities denoted by the letters. That is, the structure of the equation is examined by taking it as a complicated compound relation and by factoring it into components consisting of simpler relations. Descartes cites this as the basic task of algebra. Therein one sees the transition to the new mode of thought, a transition already embodied in the change in the name of the discipline itself. What in the sixteenth century still bears the name "algebra, sive ars rei et census", in the seventeenth century is called "algebra, seu doctrina aequationum".²⁵

At the same time, the intuitive aspects of algebra diminish. According to Descartes (Geometry, Book III), every equation xⁿ + a₁x^n-1 + . . . + a_n = 0 is a complex relation that consists of the simpler relations x-a = 0, x-b = 0, ... , x-s = 0. Each quantity a, b, c,...s is a root of the original equation, that is, each may be substituted for x without disturbing the equality. From experience, however, Descartes knows that quite often not all roots of a given equation can be found numerically or geometrically. For example, if one tries to factor the equation x³ - 1 = 0 into the form (x - a) (x - b) (x - c) = 0, one finds a = 1, of course, but no values at first for b and c. Nevertheless such values must exist or at least be imagined in order for the structural analysis of the equation to retain its generality. Hence, Descartes summons his "imaginary" roots into existence.²⁶ He does not say much more about these roots, but it suffices for our purposes that they exist at all. For, for the first time there appear new, purely abstract, non-intuitive objects in mathematics, which arise out of structural considerations.²⁷ Descartes also frees the concept of number from its classical intuitive foundations.²⁸ From his analysis of the structure of algebraic equations it follows that algebra is generally applicable to numerical problems only if the concept of "number" includes, in addition to the integers, fractions and irrationals as well.

There are other examples. From Viète's theory of equations, for example, Fermat derives the theorem that, if P(a) is an extreme value of the algebraic polynomial P(x), then P(x) must be of the form (x - a)²R(x); from this result he develops a method for determining extreme values.²⁹ Later, he derives from Descartes' theory of equations the criterion for the nature of the extreme, that is, whether a maximum or a minimum.³⁰ His technique of reduction, by which one may determine if a curve defined by an equation can be integrated algebraically, is also based on the theory of equations as a model.³¹ Not only the brilliant techniques of solution, but the very way problems are stated, show that the main characteristics of the algebraic mode of thought (and thereby the transition from the classical geometric mode) were already present in the first half of the seventeenth century. The success and spread of Fermat's and Descartes' methods made these characteristics the developmental themes of mathematics itself at the time.

Now the historically more interesting and more difficult question arises as to why this transition took place at all, and why precisely at the time it did? Of course, the question makes sense only on the presupposition that the development was not in some way predetermined, that it did not, so to speak, lay inherent in the nature of mathematics itself. Then it would merely be a question of the timing of its appearance. But mathematics is not discovered; it is invented, it is created. Symbolic algebra and the mode of thought belonging to it are creations of the seventeenth century and therefore require an historical explanation that goes beyond the timing of their appearance, especially since they differ essentially from the mathematics created by the Greeks. In addition, it seems clear that the complete explanation cannot be found within mathematics alone. The transition to the algebraic mode of thought was not a purely internal development. Why not?

The answer lies in the name that algebra bore in the seventeenth century: the ars analytica, the "analytic art". For Aristotle and for the Greek mathematicians whose works contributed so essentially to the efflorescence of mathematics in the sixteenth century, mathematics was not an art, not a technê, but a science, an epistêmê.³² That algebra and, with it (at least since Mete), mathematics itself comes to be seen and designated as an art cannot be explained from within mathematics. Second, although analysis was already held by the Greeks to be constituent part of mathematics, in antiquity it represented only a heuristic means.³³ Only what had been proved by strict synthetic deduction by means of Aristotelian logic counted as epistêmê, as science. It is clear why. Analysis assumes that the theorem to be proved is true or that the construction to be carried out has been completed and then pursues the consequences of that assumption back to an already proved theorem or an already known construction. For rigor's sake, however, one must then check to be sure that all the consequences hold in reverse, and that is the purpose of synthetic proof. What one finds in the seventeenth century-and in ever-growing measure-is analysis in the form of algebra, but without synthesis.³⁴ Hand-in-hand with assurances that an algebraic derivation can always be reversed to yield a strict synthetic proof,³⁵ the opinion is also expressed that algebra has its own form of rigour. Hence, one finds in the seventeenth century a new style of mathematics which has as a characteristic a certain relaxation of the traditional demand for rigor. (How else could an infinitesimal calculus resting on such shaky grounds have enjoyed such a rapid spread despite the objections of a Berkeley?) Since the Greek texts were still being read, this new style bears witness to a new conception of mathematics, a conception that had to be conditioned by outside forces.

Two general intellectual tendencies of the sixteenth and seventeenth centuries could have contributed essentially to such a conception of mathematics: the pedagogy of Peter Ramus and the search for a cbaracteristica universalis, a universal symbolism. The two tendencies have different roots in antiquity and in the Middle Ages. The ideas of Ramus are rooted in the rhetorical tradition of Cicero, which breathed new life into Renaissance humanism, and in the scholastic liberal arts curriculum.³⁶ A universal symbolism was the goal of the philosophy of Ramon Lull in the thirteenth century and continued from that time as part of a quasi-magical tradition that demonstrably influenced Francis Bacon.³⁷ The two tendencies were united by Ramus, in whose thought the universal symbolism lost its connection with magic in favor of a new role as a symbolic "art of memory" or means of intuition. Beyond Ramus, indeed probably through his influence, traces of these tendencies can be found in the works of Descartes and later Leibniz. Descartes and Leibniz were mathematicians; they not only did mathematics, they shaped it.

But let us go back to Ramus, the leading pedagogue of the sixteenth century. How could he have influenced mathematics? Let us look at the overall situation of mathematics before his appearance. At the universities, the first six books of Euclid's Elements were being read as preparation for Ptolemaic astronomy. There the classical tradition of Greek mathematics was fostered. Algebra as the "art of the coss" was pursued elsewhere (with few exceptions, outside of the universities), for it counted as art, not as science.³⁸ Beyond that, algebra was taken to be a sort of arithmetical solution technique, not for scientific arithmetic (that is, number theory), but for "logistic", or computational arithmetic. That is, algebra was the concern of the merchant, not of the scholar.

Ramus seems to have been the first to suggest that algebra deserved greater importance. For he maintained that algebra underlay certain parts of the second and sixth books of Euclid's Elements, as well as the famous geometrical analysis of the Greek writers.³⁹ That is, long before Zeuthen and Tannery we owe to Ramus the concept of a geometric algebra of the Greeks. According to Ramus, algebra was only a vulgar (Descartes later said "barbaric") name for a sort of analytic mathematics that the Greeks had used; traces of it were to be found, on the one hand, in Euclid and Pappus and, on the other hand, in Diophantus.⁴⁰ Descartes shared this opinion, at least in his Rules for the Direction of the Mind.⁴¹

But the geometrical analysis of the Greeks has its own history. Largely lost during the Middle Ages, it reappeared in the sixteenth century, in particular with Commandino's Latin translation of Pappus' Mathematical Collection and of the works of Archimedes.⁴² Only toward the end of the sixteenth century did mathematicians gain a clear picture of the extent of the Greek achievements in the realm of higher geometry, and the analytic methods that Pappus pointed to presented the opportunity at least to emulate these achievements. Mathematicians began to search for these analytic methods, and Ramus' suggestion that their roots lay in algebra was eagerly adopted-by Viète, by Descartes, and by Fermat.⁴³

But the word "method" (and with the word, the concept) had taken on a new meaning from Ramus, a new meaning that is reflected in the famous Discourse on the Method of Descartes. Ramus made method a pedagogical concept.⁴⁴ Method was the means of effective teaching; through method, the teacher brought his students to a profound understanding of the subject matter. At least, that was the ideal of method. In practice, Ramus' methods worked to limit and simplify subjects: accurately transmitting Aristotle's ideas and making Aristotle understandable to young students are two different things. For example, what particularly displeased Ramus about Greek mathematics as it stood in the transmitted texts was precisely its rigour, which he took to be poor method.⁴⁵ The theorems were proved, indeed rigorously proved, but they provided neither clarity nor insight. From such texts, the students learned nothing that could lead directly to independent activity and achievement in mathematics. Ramus' answer to this problem was simple, but had a long-range effect. He represents the beginnings of the writing of textbooks. In such a textbook of the seventeenth century, the Course in Mathematics (note the title) of Pierre Hérigone,⁴⁶ the Elements themselves are not reprinted, but rather their content is reformulated pedagogically and recorded for teaching purposes. For the sake of good pedagogy, this content is, so to speak, loosed from its Greek context and presented in a new form, a new form that assigns to rigour a less important role than formerly.

What does a philosopher say to this? What does Descartes say? He writes in his Second Reply to Objections against the Meditations (1641):

I distinguish two things in the geometric mode of writing, namely the order and the method of demonstration (ratio demonstrandi) . . . . There are, moreover, two methods of demonstration, one via analysis and one via synthesis.
Analysis reveals the true way in which a thing was found methodically and, as it were, a priori so that, if the reader wishes to follow it and pay sufficient attention to everything, he will understand the matter no less perfectly and make it no less his own than if he himself had found it. But it has nothing by which to incite belief in the less attentive or hostile reader. For if he should not perceive the very least thing brought forward, the necessity of its conclusions will not be clear; often it scarcely touches on many things which should be especially noted, because they are clear to the sufficiently attentive reader.
Conversely, synthesis clearly demonstrates, in a way opposite to analysis and, as it were, a posteriori (even though the proof itself is often more a priori in the former than in the latter), what has been concluded, and it uses a long series of definitions, postulates, axioms, theorems, and problems, so that, if one of the consequents is denied, it may at once be shown to be contained in the antecedents. Thus it forces assent from the reader, however hostile or stubborn. But it is not as satisfying as analysis; it does not content the minds of those wanting to learn, because it does not teach the manner in which the thing was found.
The ancient mathematicians used to employ only synthesis in their writings, not because they were simply ignorant of the other, but, as I see it, because they made so much of it that they reserved it as a secret for themselves alone.
In fact, I have followed in my Meditations only analysis, which is the true and best way of teaching....⁴⁷

We could adduce here similar passages from the works of Viète or Leibniz,⁴⁸ but the introduction to the most widely circulated textbook of algebra in the seventeenth century, the Key to Mathematics of William Oughtred, probably offers the most conclusive documentation:

When some time ago I served in the family of the recent illustrious Count of Arundel and Surrey to teach each of his children the mathematical disciplines, I composed a certain order of teaching which seemed to me most appropriate to the mathematical mysteries, such that the minds of the students who followed it would be imbued with these sciences not lightly or superficially but intimately and basically. At the request of many learned men, especially the most noble and erudite Lord Charles Cavendish, I first published this order of mine under the title of The Key to Mathematics. This treatise was not written according to the synthetic method (as is commonly done), by theorems and problems with a wide expanse of words, but according to the analytic way of invention (so that the whole is as a continuous demonstration joined together by the most firm connections), set forth not in words but in the species of things.⁴⁹

As has been said, this pedagogical motif can be documented on the basis of other examples, and it should not surprise us all that much. One characteristic of the intellectual world of the sixteenth and seventeenth centuries is precisely the extension of the school and university system to include broader segments of society. It would be surprising if this development had not influenced mathematics as the core of any study.

Now what about the second tendency mentioned above, the search for a universal symbolism? As has been said, this tendency stemmed from the high Middle Ages; in the sixteenth and seventeenth centuries, however, it enjoyed ever increasing importance. One reason for this may well be the effects of the invention of printing and the spread of the printed book. What happened then was less a question of quantity than of quality, for the printed book entailed that man now used his eyes instead of his ears for learning.⁵⁰ Where one earlier had had to rely on one's memory, one could now spare that memory. What earlier had to be stored in the brain could now be found in the library. We have already pointed to the phenomenon of the textbook. Only in a world of the eye could the search for a universal symbolism yield mature fruit.

Of what should such a symbolism consist? Listen again to Descartes:

Those things that do not require the present attention of the mind, but which are necessary to the conclusion, it is better to designate by the briefest symbols (nota) than by whole figures: in this way the memory cannot fail, nor will thought in the meantime be distracted by these things which are to be retained while it is concerned with other things to be deduced . . . . By this effort, not only will we make a saving of many words, but, what is most important, we will exhibit the pure and bare terms of the problem such that while nothing useful is omitted, nothing will be found in them which is superfluous and which vainly occupies the capacity of the mind, while the mind will be able to comprehend many things together.⁵¹

The universal symbolism desired by Lull or even by Leibniz was probably a chimera, but the search for such a symbolism meant that in the seventeenth century one would surely be found for mathematics. Roughly put, mathematicians were ready to overlook many weaknesses in symbolic algebra-as, for example, the lack of total rigour-because this algebra represented at least a part of a universal symbolism. In this regard, algebra served as a model. In his Essay Concerning Human Understanding, John Locke, for example, said:

They that are ignorant of algebra cannot imagine the wonders in this kind that are to be done by it; and what further improvements and helps, advantageous to other parts of knowledge, the sagacious mind of man may yet find out, it is not easy to determine. This at least 1 believe: that the ideas of quantity are not those alone that are capable of demonstration and knowledge; and that other and perhaps more useful parts of contemplation would afford us certainty, if vices, passions, and domineering interest did not oppose or menace such endeavours . . . . The relation of other modes may certainly be perceived, as well as those of number and extension; and I cannot see why they should not also be capable of demonstration, if due methods were thought on to examine or pursue their agreement or disagreement.⁵²

During the next two centuries a development does take place, which might be called the "algebraicization of mathematics". We see a suppression of intuitive geometry in favour of an abstract algebra. Poncelet and Plucker translate projective geometry into an algebraic form. In the lifetime of one man, Gauss, non-Euclidean geometry moves from its originally geometric, intuitive form into analytic algebraic differential geometry. With each step, the mathematician looses himself from the intuitive physical world and enters into an abstract mathematical world, into a world of structures.

Precisely how this development took place must still be determined. To start with one will have to be sure about the extent to which it sprang from internal tendencies and needs of mathematics. Hans Wussing's history of the development of the abstract concept of a group, and Michael J. Crowe's study of the emergence of vector algebra, represent examples of such internal analysis.⁵³ But one may doubt that historians will find the whole story within mathematics. Mighty figures, such as Kant, to name just one, to some extent opposed such a development. Who or what counter-balanced their influence? When even a chemist like Lavoisier introduces his Nomenclature of Chemistry with the words: "Algebra is the analytical method par excellence; it was invented to facilitate the labors of the mind, to compress into a few lines what would take pages to discuss, and to lead, finally, in a more convenient, prompt, and certain manner to the solution of very complicated questions",⁵⁴ one may assume that the algebraicization of mathematics did not take place in a vacuum, but rather in a continuous, reciprocal interaction with the surrounding culture. The precise nature of this interaction awaits the research of historians.

2. One may cite here as only one example the concept of adaequalitas, which served as the most important foundation of Fermat's method of determining extreme values and tangents to a curve and which signified a procedure that was alien to the Ancients.

3. In the Fourth Rule of the then still unpublished Regulae (composed ca. 1628) as well as in the Replies to Objections to the Meditations set out in his correspondence beginning in 1641; see Charles Adam and Paul Tannery (eds.), Oeuvres de Descartes, X, pp. 376ff (hereafter, AT) (HR, 1, pp. 12ff).

4. See, in particular, the first book of the Géométrie (Leiden, 1637), where this opinion is repeatedly expressed.

5. See M. S. Mahoney, The Royal Road: The Development of Algebraic Analysis from 1550 to 1650, with Special Reference to the Work of Pierre de Fermat (Ph. D., Princeton, 1967), Chapter III.

6. Thus, for example, John Wallis: "... not only Archimedes, but nearly all the ancients so hid from posterity their method of analysis (though it is clear that they had one) that more modern mathematicians found it easier to invent a new analysis than to seek out the old". Quoted by T. L. Heath, History of Greek Mathematics, Vol. 11 (Oxford, 1921), p. 21.

7. One might think, for example, of the modern integral calculus or of modern mathematical logic, where complicated processes are often represented symbolically and one in practice computes with symbols according to certain rules.

8. Category theory represents perhaps the newest development in this direction.

9. The decisive breakthrough takes place with the development of non-Euclidean geometry in the nineteenth century and is completed by the axiomatics that arises at the end of that century.

10. In this respect the symbolism of the German and Italian cossists of the late Middle Ages signifies no essential advance; it also consists merely of abbreviations.

11. In P. Tannery, "L'Arithmétique pythagoricienne", Bull. Sci. Math. (1885), p. 86; quoted by L. Brunschvicq, Les étapes de la philosophie mathématique (Paris, 1947), p. 103.

12. The best example is probably Viète's and Descartes' theory of equations. The derivation of the elementary symmetric functions, for example, presupposes (at least historically) the possibility of distinguishing symbolically between unknowns (variables) and constant parameters of an equation.

13. See M. S. Mahoney, "Another Look at Greek Geometrical Analysis", Archive for History of Exact Sciences, 5 (1968), pp. 318-48; esp. pp. 331-7.

14. Although a couple of theorems of relational logic occur in the Organon, for example, syllogismi obliqui, they did not belong to the scientific theory of the syllogism, that is, to analysis. See I. M. Bochenski, Formale Logik (Freiburg/Munich, 1956), pp. 101-14. Bochenski counts the logic of relations among the achievements of modern logical research; see ibid. p. 434.

15. A. Szabò, Anfänge der griechischen Mathematik (Munich/Vienna, 1969), Teil III, does not share this opinion. But his very arguments for the abstractness, or more exactly the transition to abstractness, of Greek mathematics in the fifth century B.C. point to a strong dependence on physical experience; for example, in the role of the physical intuition of motion in the concept of straight lines and planes.

16. Descartes, Géométrie, 315ff (opening of Book II).

17. Viète, In artem analyticen isagoge (Tours, 1591), p. 7: "Quod opus, ut arte aliqua juvetur, symbolo constanti & perpetuo ac bene conspicuo datae magnitudines ab incertis quesititiis distinguantur, utpote magnitudines quaesititias elemento A aliave litera vocali, E, 1, O, V, Y, datas elementis B, G, D, alliisve consonis designando."

18. See inter alia P. Treutlein, "Die deutsche Coss", Abhandlungen zur Geschichte der Mathematik, Heft 2 (1879), pp. 1-124, and J. Tropfke, Geschichte der Elementar-Mathematik, Vol. II (Berlin, 1933), Chapter A.

19. Plethos monadon aoriston; see P. Tannery (ed.) Diophantus: Arithmeticorum libri sex, (Leipzig, 1893), 6.

20. Isagoge, p. 5: "Logistice numerosa est quae per numeros, Speciosa quae per species seu rerum formas exhibetur, ut pote per Alphabetica elements. Logistices speciosae canonica praecepta sunt quatuor, ut numerosae ... . Magnitudinem magnitudini addere . . . . Magnitudinem magnitudini subducere . . . . Magnitudinem in magnitudinem ducere . . . . Magnitudinem magnitudini adplicare."

21. Whether and how Descartes was influenced by his mathematical predecessors remains unclear. However, the development of his thoughts about algebra, which can be traced in his Oeuvres, leads to the fairly certain conclusion that the independence he claimed from Viète was, in fact, the case.

22. Regulae, Rule XVI; AT, X, pp. 456ff. In the rule itself Descartes employs another symbolism, which is a transitional stage between the toss and his ultimate system of x, y, z: unknowns are designated by small letters, knowns by capitals.

23. Géométrie, Book I, pp. 297-300: "Comment le calcul d'Arithmetique se rapporte aux operations de Géométrie."

24. Géométrie, pp. 297ff: "Ainsi n'a-t-on autre chose à faire en Géométrie touchant les lignes qu'on cherche, pour les preparer à être connues, que leur en ajouter d'autres, ou en tirer, ou bien en ayant une, que je nommerai l'unité pour la rapporter d'autant mieux aux nombres, et qui peut ordinairement être prise à discretion, puis en ayant encore deux autres, en trouver une quatrième, qui soit à l'une de ces deux, comme l'autre est à l'unite cc qui est le mime que la multiplication; ou bien en trouver une quatrième, qui soit à l'une de ces deux, comme l'unite est à l'autre, ce qui est le même que la division; ou enfin trouver une, ou deux, ou plusieurs moyennes proportionelles entre l'unité et quelque autre ligne, ce qui est le même que tirer la racine carrée ou cubique, etc. Et je ne craindrai pas d'introduire ces termes d'Arithmétique en la Géométrie, afin de me rendre plus intelligible. [So too in geometry, to find required lines it is merely necessary to add or subtract other lines; or else, taking one line which I shall call unity in order to relate it as closely as possible to numbers, and which can in general be chosen arbitrarily, and having given two other lines, to find a fourth line which shall be to one of the given lines as the other is to unity (which is the same as multiplication); or, again, to find a fourth line which is to one of the given lines as unity is to the other (which is equivalent to division); or finally, to find one, two, or several mean proportionals between unity and some other line (which is the same as extracting the square root, cube root, etc. of the given line). And I shall not hesitate to introduce these arithmetical terms into geometry, for the sake of greater clearness." [(D. E. Smith and M. L. Latham (trans), The Geometry of René Descartes (New York, 1954), pp. 2-5)] Particularly important here is the last sentence, which shows clearly that Descartes was aiming not at the arithmetization of geometry, but rather at an algebraicization of geometry.

25. Algebra, or the Doctrine of Equations was, for example, the title of a work by Richard Balam, published in London in 1650 and 1653.

26. Géométrie, Book Ill, p. 380: "Au reste tant les vraies racines que les fausses ne sont pas toujours réeles mais quelquefois seulement imaginaires; c'est à dire qu'on peut bien toujours en imaginer autant que j'ai dit en chaque équation; mais qu'il n'y a quelquefois aucune quantité, qui corresponde àcelles qu'on imagine." [Neither the true nor false roots are always real; sometimes they are imaginary; that is, while we can always conceive of as many roots for each equation as I have already assigned, yet there is not always a definite quantity corresponding to each root so conceived of.] [D. E. Smith and M. L. Latham (trans), op. cit. p. 175)]

27. To be sure, one finds already in the sixteenth century solutions that contain the root of a negative number, but precisely as solutions of particular individual equations. Descartes makes "imaginary" solutions general and in fact establishes them on structural grounds.

28. See J. Klein, Greek Mathematical Thought and the Origin of Algebra (Cambridge, Mass., 1968).

29. See Ch. Henry and P. Tannery (eds), "Analytica eiusdem methodi [de maxima et minima] investigatio", Oeuvres de Fermat, Vol. I (Paris, 1891), pp. 147-53, where the essay is reproduced under the title "De maxima et minima".

30. See letter to Brulart de St.-Martin, 31. III[?]. 1643, C. Waard (ed.), Oeuvres, Supplement, Paris, 1922, pp. 120-5.

31. In De aequationum localium transmutatione et emendatione ad multimodam curvilineorum inter se vel cum rectis comparationem, cui annectitur proportionis geometricae in quadrandis infinitis parabolis et hyperbolis usus, Oeuvres, I, pp. 255-85. The title appears to have arisen from a conscious borrowing from Viète's works on the theory of equations, De aequationum recognitione et emendatione tractatus duo (composed ca. 1593, publ. Paris, 1615, and Leiden, 1646).

32. On the concept of epistêmê in early Greek mathematics, see P.-H. Michel, De Pythagore à Euclide (Paris, 1950), p. 22.

33. See M. S. Mahoney, "Another Look at Greek Geometrical Analysis", op. cit.

34. Fermat (at least where he proceeds algebraically) and Descartes are outstanding examples of this.

35. In addition to Descartes (see below), Viète, Isagoge, Chapter VI and Marino Ghetaldi, De resolutione et compositione mathematica (Rome, 1630), I, pp. 1ff.

36. On this subject, see W. J. Ong, Ramus: Method and the Decay of Dialogue (Cambridge, Mass., 1958).

37. On this subject, see P. Rossi, Clavis Universalis (Milan/Naples, 1960).

38. Beginning in the mid-fifteenth century there are exceptions to this rule, in particular at various German universities. By and large, however, algebra developed outside the universities, and the history of its introduction into the university curriculum remains as yet undetermined.

39. For example, Ramus, in his Geometriae libri septem et viginti (Basel, 1569), p. 6 (of the Frankfurt, 1627, edition), sets out the algebraic content of Euclid, 11, 4 - (a + b)² = a² + b² + 2ab - by means of a numerical example and then remarks, ". . . hic geometriae analyseos usus superest".

40. Ramus, Scholarum mathernaticarum libri unus et triginta (Paris, 1569; Frankfurt, 1627), Book 1, 35: "Sed ex his, quorum scripta superant, praecipuus est Pappus: . . . Diophantus cujus sex libros, cum tamen author ipse tredecim polliceatur, graecos habemus de arithmeticis admirandae subtilitatis artem complexis, quae vulgo Algebra arabico nomine appellatur: cum tamen ex authore hoc antiquo (citatur enim a Theone) antiquitas artis appareat."

41. See Regulae, Rule IV; AT, X, pp. 376ff (HR, I, pp. 12ff).

42. Pappus (Pisa, 1588, edition) thereafter counted among the most widely read classical texts. It served, for example, as point of departure (and even as initial stimulus) for several of Fermat's investigations.

43. See M. S. Mahoney, Royal Road, Chapter Ill.

44. See W. J. Ong, Ramus, Chapter VII, XI.

45. Thus Ramus in Book Ill of his Scbolae mathematicae often takes Euclid severely to task for the poor method of the Elements.

46. Four volumes in three publications (Paris, 1634-37); and Supplement (Paris, 1642).

47. AT, VII, p. 155 (HR, II, pp. 48-9).

48. The pertinent passages for Leibniz would be those concerning his characteristica universalis.

49. William Oughtred, Clavis mathematicae denuo limata sive potius fabricata (Oxford, fifth edition, 1693), Introduction (added to third edition). Oughtred then goes on to speak of the usefulness of algebra in understanding Euclid, Archimedes, Apollonius, and Diophantus and in solving the most difficult problems.

50. W. J. Ong's interpretation of Ramist thought is based in part on this transition from ear to eye.

51. Regulae, Rule XVI; AT, X, p. 454 (HR, 1, p. 66).

52. John Locke, Essay of Human Understanding (1690), quoted by H. J. Kearney, Origins of the Scientific Revolution (London, 1965), pp. 131ff.

53. Berlin, 1969, and South Bend, Ind., 1967.

54. Quoted by C. C. Gillispie, The Edge of Objectivity (Princeton, 1960), p. 245.