The Platonic solids are polyhedra with regular polygon faces. Faces and vertices are identical. There are only five of then, shown below.
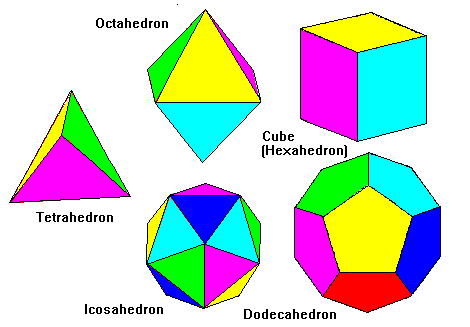
| Solid | Faces | Edges of Face | Vertices | Edges at Vertex | Edges | Dual of... | ||
|---|---|---|---|---|---|---|---|---|
| Tetrahedron | 4 | 3 | 4 | 3 | 6 | Tetrahedron | ||
| Cube | 6 | 4 | 8 | 3 | 12 | Octahedron | ||
| Octahedron | 8 | 3 | 6 | 4 | 12 | Cube | ||
| Dodecahedron | 12 | 5 | 20 | 3 | 30 | Icosahedron | ||
| Icosahedron | 20 | 3 | 12 | 5 | 30 | Dodecahedron |
Note that in each case, Euler's Rule is followed: F + V = E + 2. Also note that faces in the cube and vertices in the octahedron play similar roles, and similarly for the dodecahedron and icosahedron. These solids are duals of each other.
Platonic solids and uniform tilings are closely related as shown below. Starting from the tetrahedron we have polyhedra with three triangles, squares and pentagons at each vertex. The next step is the plane tiling with three hexagons at each vertex. Also starting from the tetrahedron we have polyhedra with three, for and five triangles at each vertex. The next step is the plane tiling with six triangles at each vertex. The figures in the top and bottom rows are duals of each other.
In addition to the convex Platonic solids, there are four other solids with identical faces and vertices. In these solids the faces penetrate through each other. These are the Kepler-Poinsot Solids.
Return to Symmetry Index
Return to Professor Dutch's Home page
Created 2 Oct. 1997, Last Update 2 Oct. 1997
Not an official UW Green Bay site