|
|
|
|
|
|
|
|
|
|
|
|
Pythagorean Theorem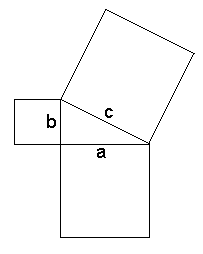
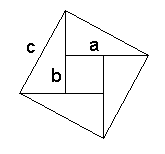
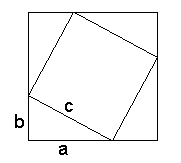
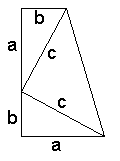
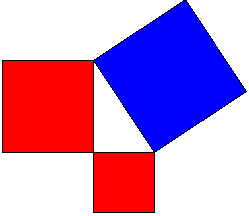
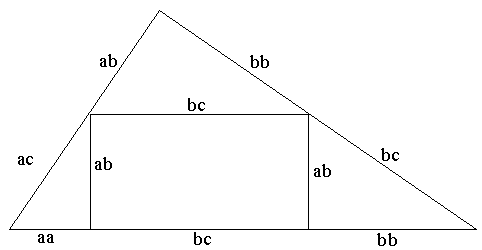
Let's build up squares on the sides of a right triangle. Pythagoras' Theorem then claims that the sum of (the areas of) two small squares equals (the area of) the large one. In algebraic terms, a2 + b2 = c2 where c is the hypotenuse while a and b are the sides of the triangle. The theorem is of fundamental importance in the Euclidean Geometry where it serves as a basis for the definition of distance between two points. It's so basic and well known that, I believe, anyone who took geometry classes in high school couldn't fail to remember it long after other math notions got solidly forgotten. I plan to present several geometric proofs of the Pythagorean Theorem. An impetus for this page was provided by a remarkable Java applet written by Jim Morey. This constitutes the first proof on this page. One of my first Java applets was written to illustrate another Euclidean proof. Presently, there are several Java illustrations of various proofs, but the majority have been rendered in plain HTML with simple graphic diagrams. Remark
Proof #2
We start with two squares with sides a and b, respectively, placed side by side. The total area of the two squares is a2+b2.
The construction did not start with a triangle but now we draw two of them, both with sides a and b and hypotenuse c. Note that the segment common to the two squares has been removed. At this point we therefore have two triangles and a strange looking shape.
As a last step, we rotate the triangles 90o, each around its top vertex. The right one is rotated clockwise whereas the left triangle is rotated counterclockwise. Obviously the resulting shape is a square with the side c and area c2. (A variant of this proof is found in an extant manuscript by Thâbit ibn Qurra located in the library of Aya Sofya Musium in Turkey, registered under the number 4832. [R. Shloming, Thâbit ibn Qurra and the Pythagorean Theorem, Mathematics Teacher 63 (Oct., 1970), 519-528]. ibn Qurra's diagram is similar to that in proof #27. The proof itself starts with noting the presence of four equal right triangles surrounding a strangenly looking shape as in the current proof #2. These four triangles correspond in pairs to the starting and ending positions of the rotated triangles in the current proof. This same configuration could be observed in a proof by tesselation.)
Proof #3
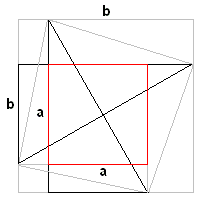
Now we start with four copies of the same triangle. Three of these have been rotated 90o, 180o, and 270o, respectively. Each has area ab/2. Let's put them together without additional rotations so that they form a square with side c.
The square has a square hole with the side
Proof #4
The fourth approach starts with the same four triangles, except that, this time, they combine to form a square with the side (a+b) and a hole with the side c. We can compute the area of the big square in two ways. Thus
simplifying which we get the needed identity.
Proof #5
This proof, discovered by President J.A. Garfield in 1876 [Pappas], is a variation on the previous one. But this time we draw no squares at all. The key now is the formula for the area of a trapezoid - half sum of the bases times the altitude - (a+b)/2·(a+b). Looking at the picture another way, this also can be computed as the sum of areas of the three triangles - ab/2 + ab/2 + c·c/2. As before, simplifications yield a2+b2=c2. Two copies of the same trapezoid can be combined in two ways by attaching them along the slanted side of the trapezoid. One leads to the proof #4, the other to proof #52.
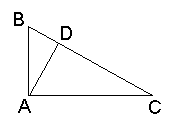
Proof #6
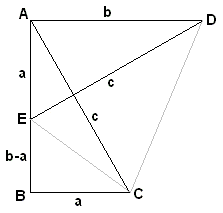
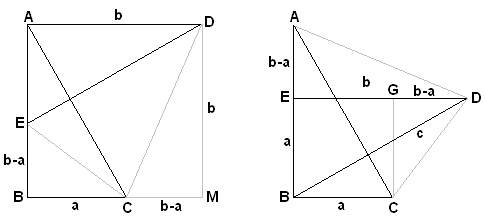
We start with the original triangle, now denoted ABC, and need only one additional construct - the altitude AD. The triangles ABC, BDA and ADC are similar which leads to two ratios:
Written another way these become
Summing up we get
In a private correspondence, Dr. France Dacar, Ljubljana, Slovenia, has suggested that the diagram on the right may serve two purposes. First, it gives an additional graphical representation to the present proof #6. In addition, it highlights the relation of the latter to proof #1.
Proof #7The next proof is taken verbatim from Euclid VI.31 in translation by Sir Thomas L. Heath. The great G. Polya analyzes it in his Induction and Analogy in Mathematics (II.5) which is a recommended reading to students and teachers of Mathematics. In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle. Let ABC be a right-angled triangle having the angle BAC right; I say that the figure on BC is equal to the similar and similarly described figures on BA, AC. 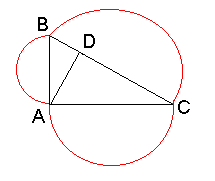
Let AD be drawn perpendicular. Then since, in the right-angled triangle ABC, AD has been drawn from the right angle at A perpendicular to the base BC, the triangles ABD, ADC adjoining the perpendicular are similar both to the whole ABC and to one another [VI.8]. And, since ABC is similar to ABD, therefore, as CB is to BA so is AB to BD [VI.Def.1]. And, since three straight lines are proportional, as the first is to the third, so is the figure on the first to the similar and similarly described figure on the second [VI.19]. Therefore, as CB is to BD, so is the figure on CB to the similar and similarly described figure on BA. 
For the same reason also, as BC is to CD, so is the figure on BC to that on CA; so that, in addition, as BC is to BD, DC, so is the figure on BC to the similar and similarly described figures on BA, AC. But BC is equal to BD, DC; therefore the figure on BC is also equal to the similar and similarly described figures on BA, AC. Therefore etc. Q.E.D. ConfessionI got a real appreciation of this proof only after reading the book by Polya I mentioned above. I hope that a Java applet will help you get to the bottom of this remarkable proof. Note that the statement actually proven is much more general than the theorem as it's generally known.
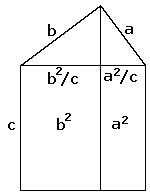
Proof #8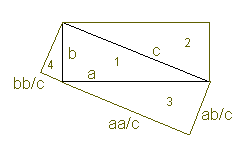
Playing with the applet that demonstrates the Euclid's proof (#7), I have discovered another one which, although ugly, serves the purpose nonetheless. Thus starting with the triangle 1 we add three more in the way suggested in proof #7: similar and similarly described triangles 2, 3, and 4. Deriving a couple of ratios as was done in proof #6 we arrive at the side lengths as depicted on the diagram. Now, it's possible to look at the final shape in two ways:
Equating areas leads to
Simplifying we get
RemarkIn hindsight, there is a simpler proof. Look at the rectangle (1+3+4). Its long side is, on one hand, plain c, while, on the other hand, it's a2/c+b2/c and we again have the same identity.
Proof #9
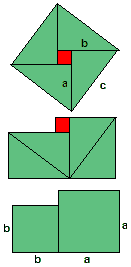
Another proof stems from a rearrangement of rigid pieces, much like proof #2. It makes the algebraic part of proof #4 completely redundant. There is nothing much one can add to the two pictures. (My sincere thanks go to Monty Phister for the kind permission to use the graphics.) There is an interactive simulation to toy with.
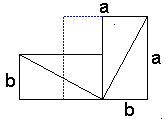
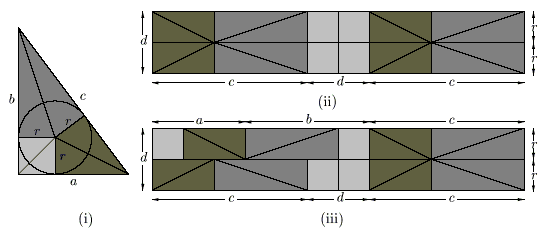
Proof #10This and the next 3 proofs came from [PWW]. The triangles in Proof #3 may be rearranged in yet another way that makes the Pythagorean identity obvious. (A more elucidating diagram on the right was kindly sent to me by Monty Phister.)
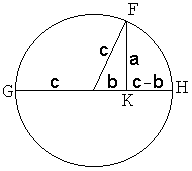
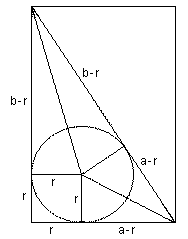
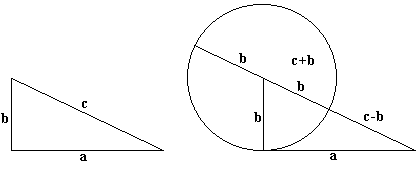
Proof #11Draw a circle with radius c and a right triangle with sides a and b as shown. In this situation, one may apply any of a few well known facts. For example, in the diagram three points F, G, H located on the circle form another right triangle with the altitude FK of length a. Its hypotenuse GH is split in the ratio (c+b)/(c-b). So, as in Proof #6, we get a2 = (c+b)(c-b) = c2 - b2.
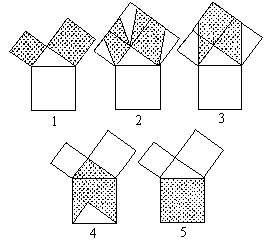
Proof #12This proof is a variation on #1, one of the original Euclid's proofs. In parts 1,2, and 3, the two small squares are sheared towards each other such that the total shaded area remains unchanged (and equal to a2+b2.) In part 3, the length of the vertical portion of the shaded area's border is exactly c because the two leftover triangles are copies of the original one. This means one may slide down the shaded area as in part 4. From here the Pythagorean Theorem follows easily. (This proof can be found in H. Eves, In Mathematical Circles, MAA, 2002, pp. 74-75)
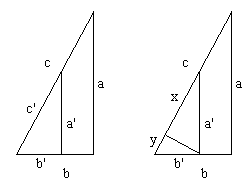
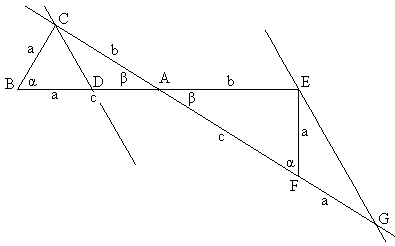
Proof #13In the diagram there is several similar triangles (abc, a'b'c', a'x, and b'y.) We successively have
And, finally, cc' = aa' + bb'. This is very much like Proof #6 but the result is more general.
Proof #14This proof by H.E.Dudeney (1917) starts by cutting the square on the larger side into four parts that are then combined with the smaller one to form the square built on the hypotenuse. Greg Frederickson from Purdue University, the author of a truly illuminating book, Dissections: Plane & Fancy (Cambridge University Press, 1997), pointed out the historical inaccuracy:
Bill Casselman from the University of British Columbia seconds Greg's information. Mine came from Proofs Without Words by R.B.Nelsen (MAA, 1993).
Proof #15This remarkable proof by K. O. Friedrichs is a generalization of the previous one by Dudeney. It's indeed general. It's general in the sense that an infinite variety of specific geometric proofs may be derived from it. (Roger Nelsen ascribes [PWWII, p 3] this proof to Annairizi of Arabia (ca. 900 A.D.))
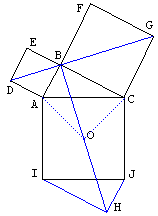
Proof #16This proof is ascribed to Leonardo da Vinci (1452-1519) [Eves]. Quadrilaterals ABHI, JHBC, ADGC, and EDGF are all equal. (This follows from the observation that the angle ABH is 45o. This is so because ABC is right-angled, thus center O of the square ACJI lies on the circle circumscribing triangle ABC. Obviously, angle ABO is 45o.) Now, area(ABHI)+area(JHBC)=area(ADGC)+area(EDGF). Each sum contains two areas of triangles equal to ABC (IJH or BEF) removing which one obtains the Pythagorean Theorem. David King modifies the argument somewhat
The side lengths of the hexagons are identical. The angles at P (right angle + angle between a & c) are identical. The angles at Q (right angle + angle between b & c) are identical. Therefore all four hexagons are identical.
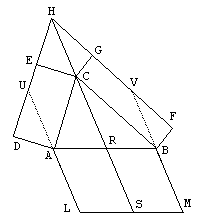
Proof #17This proof appears in the Book IV of Mathematical Collection by Pappus of Alexandria (ca A.D. 300) [Eves, Pappas]. It generalizes the Pythagorean Theorem in two ways: the triangle ABC is not required to be right-angled and the shapes built on its sides are arbitrary parallelograms instead of squares. Thus build parallelograms CADE and CBFG on sides AC and, respectively, BC. Let DE and FG meet in H and draw AL and BM parallel and equal to HC. Then area(ABML)=area(CADE)+area(CBFG). Indeed, with the sheering transformation already used in proofs #1 and #12, area(CADE)=area(CAUH)=area(SLAR) and also area(CBFG)=area(CBVH)=area(SMBR). Now, just add up what's equal.
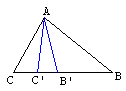
Proof #18This is another generalization that does not require right angles. It's due to Thâbit ibn Qurra (836-901) [Eves]. If angles CAB, AC'B and AB'C are equal then
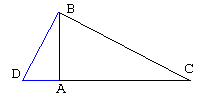
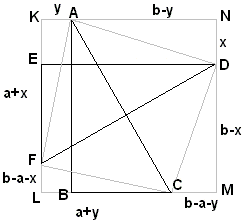
Proof #19This proof is a variation on #6. On the small side AB add a right-angled triangle ABD similar
to ABC. Then, naturally, DBC is similar to the other two. From
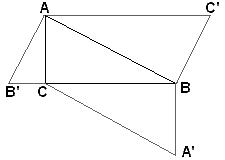
Proof #20This one is a cross between #7 and #19. Construct triangles ABC', BCA', and ACB' similar to ABC, as in the diagram. By construction,
Proof #21The following is an excerpt from a letter by Dr. Scott Brodie from the Mount Sinai School of Medicine, NY who sent me a couple of proofs of the theorem proper and its generalization to the Law of Cosines:
Proof #22Here is the second proof from Dr. Scott Brodie's letter.
Dr. Brodie also created a Geometer's SketchPad file to illustrate this proof.
Proof #23Another proof is based on the Heron's formula which I already used in Proof #7 to display triangle areas. This is a rather convoluted way to prove the Pythagorean Theorem that, nonetheless reflects on the centrality of the Theorem in the geometry of the plane.
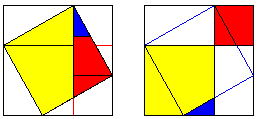
Proof #24[Swetz] ascribes this proof to abu' l'Hasan Thâbit ibn Qurra Marwân al'Harrani (826-901). It's the second of the proofs given by Thâbit ibn Qurra. The first one is essentially the #2 above. The proof resembles part 3 from proof #12.
This is an "unfolded" variant of the above proof. Two pentagonal regions - the red and the blue - are obviously equal and leave the same area upon removal of three equal triangles from each. The proof is popularized by Monty Phister, author of the inimitable Gnarly Math CD-ROM. 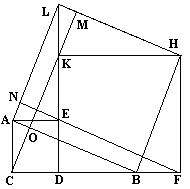
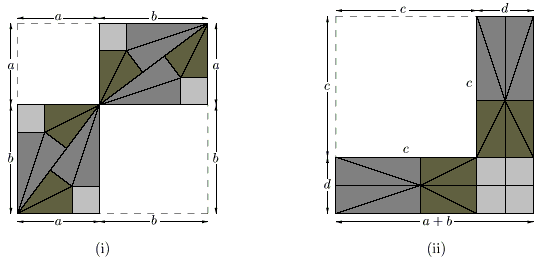
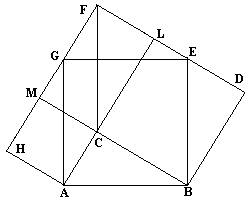
Proof #25B.F.Yanney (1903, [Swetz]) gave a proof using the "sliding argument" also employed in the Proofs #1 and #12. Successively, areas of LMOA, LKCA, and ACDE (which is AC2) are equal as are the areas of HMOB, HKCB, and HKDF (which BC2). BC = DF. Thus AC2 + BC2 = area(LMOA) + area(HMOB) = area(ABHL) = AB2.
Proof #26This proof I discovered at the site maintained by Bill Casselman where it is presented by a Java applet. With all the above proofs, this one must be simple. Similar triangles like in proofs #6 or #13. 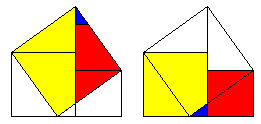
Proof #27The same pieces as in proof #26 may be rearrangened in yet another manner. This dissection is often attributed to the 17th century Dutch mathematician Frans van Schooten. [Frederickson, p. 35] considers it as a hinged variant of one by ibn Qurra, see the note in parentheses following proof #2. Dr. France Dacar from Slovenia has pointed out that this same diagram is easily explained with a tesselation in proof #15. As a matter of fact, it may be better explained by a different tesselation. (I thank Douglas Rogers for setting this straight for me.)
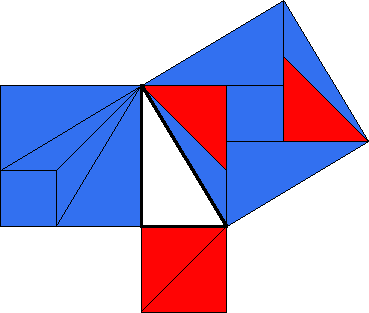
Proof #28Melissa Running from MathForum has kindly sent me a link to A proof of the Pythagorean Theorem by Liu Hui (third century AD). The page is maintained by Donald B. Wagner, an expert on history of science and technology in China. The diagram is a reconstruction from a written description of an algorithm by Liu Hui (third century AD). For details you are referred to the original page.
Proof #29A mechanical proof of the theorem deserves a page of its own. Pertinent to that proof is a page "Extra-geometric" proofs of the Pythagorean Theorem by Scott Brodie Proof #30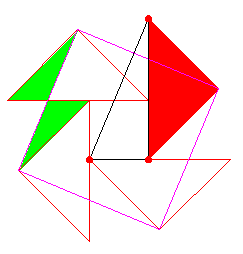
This proof I found in R. Nelsen's sequel Proofs Without Words II. (It's due to Poo-sung Park and was originally published in Mathematics Magazine, Dec 1999). Starting with one of the sides of a right triangle, construct 4 congruent right isosceles triangles with hypotenuses of any subsequent two perpendicular and apices away from the given triangle. The hypotenuse of the first of these triangles (in red in the diagram) should coincide with one of the sides. The apices of the isosceles triangles form a square with the side equal to the hypotenuse of the given triangle. The hypotenuses of those triangles cut the sides of the square at their midpoints. So that there appear to be 4 pairs of equal triangles (one of the pairs is in green). One of the triangles in the pair is inside the square, the other is outside. Let the sides of the original triangle be a, b, c (hypotenuse). If the first isosceles triangle was built on side b, then each has area b2/4. We obtain
Here's a dynamic illustration and another diagram that shows how to dissect two smaller squares and rearrange them into the big one. 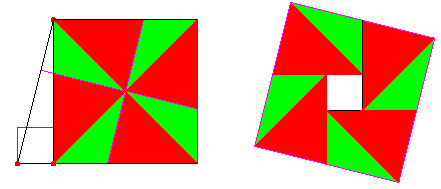 Proof #31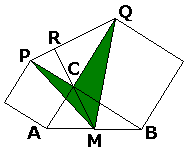
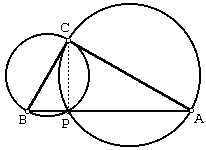
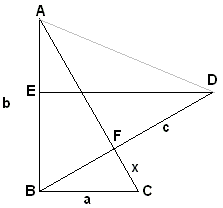
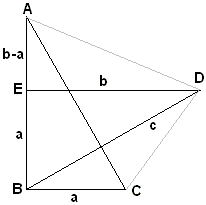
Given right The median to the hypotenuse equals half of the latter. Therefore, With these preliminaries we turn to triangles MCP and MCQ. We evaluate their areas in two different ways: One one hand, the altitude from M to PC equals AC/2 = b/2. But also We may sum up the two identities: (My gratitude goes to Floor van Lamoen who brought this proof to my attention. It appeared in Pythagoras - a dutch math magazine for schoolkids - in the December 1998 issue, in an article by Bruno Ernst. The proof is attributed to an American High School student from 1938 by the name of Ann Condit.) Proof #32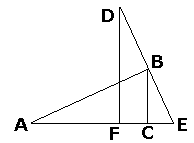
Let ABC and DEF be two congruent right triangles such that B lies on DE and A, F, C, E are collinear. Area(
(This proof is a simplification of one of the proofs by Michelle Watkins, a student at the University of North Florida, that appeared in Math Spectrum 1997/98, v30, n3, 53-54.) Douglas Rogers observed that the same diagram can be treated differently:
The next two proofs have accompanied the following message from Shai Simonson, Professor at Stonehill College in Cambridge, MA:
Proof #33
Proof #34
Proof #35Cracked Domino - a proof by Mario Pacek (aka Pakoslaw Gwizdalski) - also requires some thought.
The proof sent via email was accompanied by the following message:
The manner in which the pieces are combined may well be original. The dissection itself is well known (see Proofs 26 and 27) and is described in Frederickson's book, p. 29. It's remarked there that B. Brodie (1884) observed that the dissection like that also applies to similar rectangles. The dissection is also a particular instance of the superposition proof by K.O.Friedrichs. Proof #36This proof is due to J. E. Böttcher and has been quoted by Nelsen (Proofs Without Words II, p. 6). I think cracking this proof without words is a good exercise for middle or high school geometry class.
Proof #37An applet by David King that demonstrates this proof has been placed on a separate page. Proof #38This proof was also communicated to me by David King. Squares and 2 triangles combine to produce two hexagon of equal area, which might have been established as in Proof #9. However, both hexagons tessellate the plane. 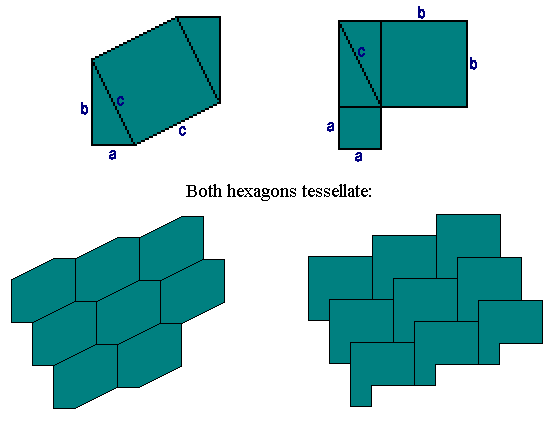 For every hexagon in the left tessellation there is a hexagon in the right tessellation. Both tessellations have the same lattice structure which is demonstrated by an applet. The Pythagorean theorem is proven after two triangles are removed from each of the hexagons. Proof #39(By J. Barry Sutton, The Math Gazette, v 86, n 505, March 2002, p72.) 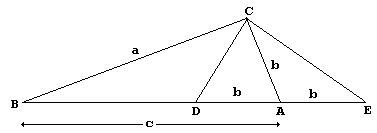 Let in By construction, C lies on the circle with center A and radius b. Angle DCE subtends its diameter and thus is right: Triangles DBC and EBC share
And finally
The diagram reminds one of Thâbit ibn Qurra's proof. But the two are quite different.
Proof #40
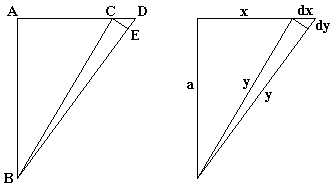
This one is by Michael Hardy from University of Toledo and was published in The Mathematical Intelligencer in 1988. It must be taken with a grain of salt. Let ABC be a right triangle with hypotenuse BC. Denote
which after integration gives y2 - x2 = const. The value of the constant is determined from the initial condition for It is easy to take an issue with this proof. What does it mean for a triangle to be
which, after subtraction, gives
For small dx and dy, dx2 and dy2 are even smaller and might be neglected, leading to the approximate The trick in Michael's vignette is in skipping the issue of approximation. But can one really justify the derivation without relying on the Pythagorean theorem in the first place? Regardless, I find it very much to my enjoyment to have the ubiquitous equation
Proof #41
This one was sent to me by Geoffrey Margrave from Lucent Technologies. It looks very much as #8, but is arrived at in a different way. Create 3 scaled copies of the triangle with sides a, b, c by multiplying it by a, b, and c in turn. Put together, the three similar triangles thus obtained form a rectangle whose upper side is Also, picking just two triangles leads to a variant of Proofs #6 and #19:
In this form the proof appears in [Birkhoff, p. 92]. Yet another variant that could be related to #8 has been sent by James F.:
The latter has a twin with a and b swapping their roles.
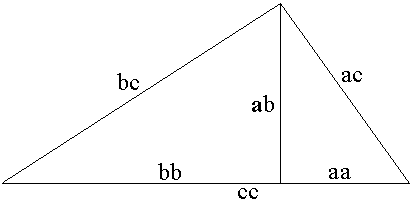
Proof #42The proof is based on the same diagram as #33 [Pritchard, p. 226-227].
Area of a triangle is obviously rp, where r is the incircle and
which is equivalent to
or
And finally
(The proof is due to Jack Oliver, and was originally published in Mathematical Gazette 81 (March 1997), p 117-118.)
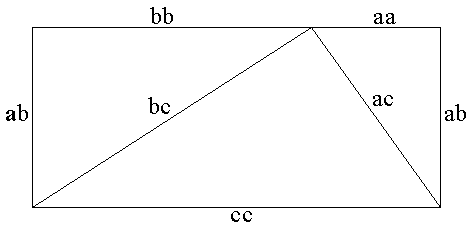
Proof #43By Larry Hoehn [Pritchard, p. 229, and Math Gazette].
Apply the Power of a Point theorem to the diagram above where the side a serves as a tangent to a circle of radius b: (The configuration here is essentially the same as in proof #39. The invocation of the Power of a Point theorem may be regarded as a shortcut to the argument in proof #39.)
Proof #44The following proof related to #39, have been submitted by Adam Rose (Sept. 23, 2004.)
Start with two identical right triangles: ABC and AFE, A the midpoint of BE and CF. Mark D on AB and G on extension of AF, such that
(For further notations refer to the above diagram.) Since We now have two lines, CD and EG, crossed by CG with two alternate interior angles, ACD and AGE, equal. Therefore, CD||EG. Triangles ACD and AGE are similar, and AD/AC = AE/AG:
and the Pythagorean theorem follows.
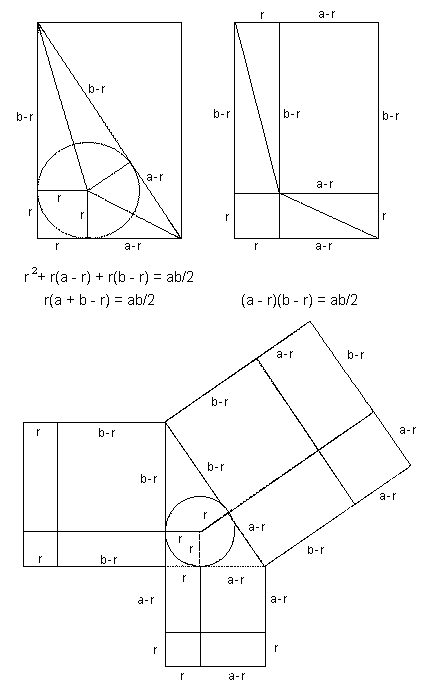
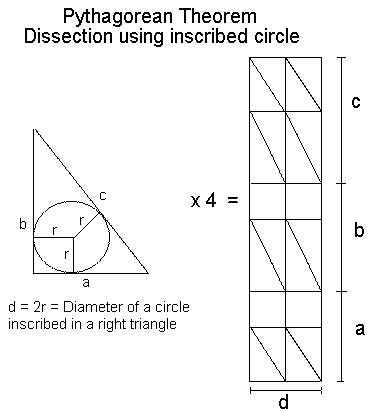
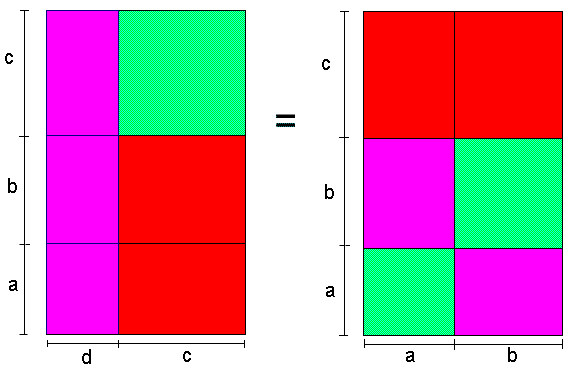
Proof #45This proof is due to Douglas Rogers who came upon it in the course of his investigation into the history of Chinese mathematics. The two have also online versions:
The proof is a variation on #33, #34, and #42. The proof proceeds in two steps. First, as it may be observed from
a Liu Hui identity (see also Mathematics in China)
where d is the diameter of the circle inscribed into a right triangle with sides a and b and hypotenuse c. Based on that and rearranging the pieces in two ways supplies another proof without words of the Pythagorean theorem:
Proof #46This proof is due to Tao Tong (Mathematics Teacher, Feb., 1994, Reader Reflections). I learned of it through the good services of Douglas Rogers who also brought to my attention Proofs #47, #48 and #49. In spirit, the proof resembles the proof #32.
Let ABC and BED be equal right triangles, with E on AB. We are going to evaluate the area of
Using the notations as indicated in the diagram we get
The two formulas easily combine into the Pythagorean identity.
Proof #47This proof which is due to a high school student John Kawamura was report by Chris Davis, his geometry teacher at Head-Rouce School, Oakland, CA (Mathematics Teacher, Apr., 2005, p. 518.)
The configuration is virtually identical to that of Proof #46, but this time we are interested in the area of the quadrilateral ABCD. Both of its perpendicular diagonals have length c, so that its area equals c2/2. On the other hand,
Multiplying by 2 yields the desired result.
Proof #48(W. J. Dobbs, The Mathematical Gazette, 8 (1915-1916), p. 268.)
In the diagram, two right triangles - ABC and ADE - are equal and E is located on AB. As in President Garfield's proof, we evaluate the area of a trapezoid ABCD in two ways:
where, as in the proof #47, c·c is the product of the two perpendicular diagonals of the quadrilateral AECD. On the other hand,
Combining the two we get c2/2 = a2/2 + b2/2, or, after multiplication by 2,
Proof #49
In the previous proof we may proceed a little differently. Complete a square on sides AB and AD of the two triangles. Its area is, on one hand, b2 and, on the other,
which amounts to the same identity as before. Douglas Rogers who observed the relationship between the proofs 46-49 also remarked that a square could have been drawn on the smaller legs of the two triangles if the second triangle is drawn in the "bottom" position as in proofs 46 and 47. In this case, we will again evaluate the area of the quadrilateral ABCD in two ways. With a reference to the second of the diagrams above,
as was desired. He also pointed out that it is possible to think of one of the right triangles as sliding from its position in proof #46 to its position in proof #48 so that its short leg glides along the long leg of the other triangle. At any intermediate position there is present a quadrilateral with equal and perpendicular diagonals, so that for all positions it is possible to construct proofs analogous to the above. The triangle always remains inside a square of side b - the length of the long leg of the two triangles. Now, we can also imagine the triangle ABC slide inside that square. Which leads to a proof that directly generalizes #49 and includes configurations of proofs 46-48. See below.
Proof #50
The area of the big square KLMN is b2. The square is split into 4 triangles and one quadrilateral:
It's not an interesting derivation, but it shows that, when confronted with a task of simplifying algebraic expressions, multiplying through all terms as to remove all parentheses may not be the best strategy. In this case, however, there is even a better strategy that avoids lengthy computations altogether. On Douglas Rogers' suggestion, complete each of the four triangles to an appropriate rectangle:
The four rectangles always cut off a square of size a, so that their total area is b2 - a2. Thus we can finish the proof as in the other proofs of this series:
Proof #51(W. J. Dobbs, The Mathematical Gazette, 7 (1913-1914), p. 168.)
This one comes courtesy of Douglas Rogers from his extensive collection. As in Proof #2, the triangle is rotated 90o around one of its corners, such that the angle between the hypotenuses in two positions is right. The resulting shape of area b2 is then dissected into two right triangles with side lengths
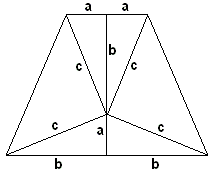
Proof #52This proof, discovered by a high school student, Jamie deLemos (The Mathematics Teacher, 88 (1995), p. 79.), has been quoted by Larry Hoehn (The Mathematics Teacher, 90 (1997), pp. 438-441.)
On one hand, the area of the trapezoid equals
and on the other,
Equating the two gives a2 + b2 = c2. The proof is closely related to President Garfield's proof.
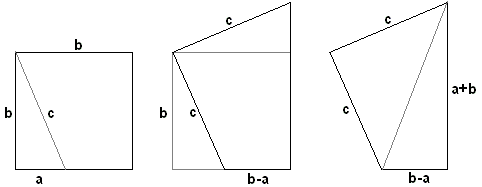
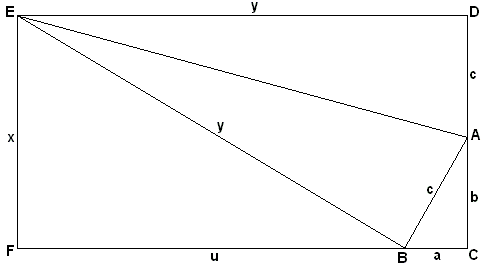
Proof #53Larry Hoehn also published the following proof (The Mathematics Teacher, 88 (1995), p. 168.):
Extend the leg AC of the right triangle ABC to D so that By this construction, triangles ABE and ADE share side AE, have other two sides equal: It then follows that in right triangles ABC and BEF angles ABC and EBF add up to 90o. Thus
The two triangles are similar, so that
But, EF = CD, or x = b + c, which in combination with the above proportion gives
On the other hand, y = u + a, which leads to
which is easily simplified to c2 = a2 + b2.
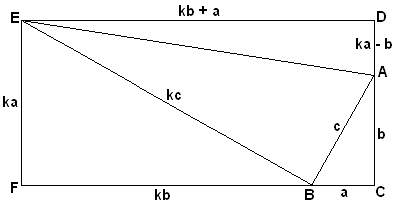
Proof #54kLater (The Mathematics Teacher, 90 (1997), pp. 438-441.) Larry Hoehn took a second look at his proof and produced a generic one, or rather a whole 1-parameter family of proofs, which, for various values of the parameter, included his older proof as well as #41. Below I offer a simplified variant inspired by Larry's work.
To reproduce the essential point of proof #53, i.e. having a right angled triangle ABE and another BEF, the latter being similar to Now, the area of the rectangle CDEF can be computed directly as the product of its sides ka and (kb + a), or as the sum of areas of triangles BEF, ABE, ABC, and ADE. Thus we get
which after simplification reduces to
which is just one step short of the Pythagorean proposition. The proof works for any value of k satisfying k Obviously, dealing with a trapezoid is less restrictive and works for any positive value of k.
References
On Internet
|
| 13853598 |
|