The Quantum Casino

Part 2 of "An Introduction to Quantum Reality"

In a nutshell, the goal of quantum mechanics is to calculate the properties (such as position and momentum) of particles. In classical physics (the physics which is generally used to describe the everyday objects around us) all objects possess properties which are an inherent part of the object. For example, for a green apple it could be said that the apple's colour "has" the property "green". Let's call these everyday objects which have clearly-defined inherent properties - such as an apple - to be "ordinary objects". In classical physics the entire physical world consists of nothing but ordinary objects.

However, as shown the previous page Quantum Mechanics: An Introduction, quantum mechanics reveals that the world is not made of these ordinary objects. Rather, it was shown that everything in the universe it is made out of rather peculiar quantum particle/wave objects. One of the key properties of a particle - its position - was only set when some sort of measurement process was applied. Before the measurement operation was applied, the particle had no clearly defined position, being stretched-out in space like a wave.

So quantum mechanics shows us that we cannot talk about an object having a particular value for a property before we take the measurement - it's as if the measurement process actually creates the property value. Even stranger than this, we will see in the discussion on this page that quantum mechanics says that we cannot tell for certain what property value will emerge when we take the measurement - all we can ever say is that the value will be a random choice from a selection of possible values!

So quantum mechanics says that at its most basic level, nature is fundamentally random. This might come as a bit of a shock to us as we are used to cause and effect following each other in a perfectly predictable, deterministic manner. This is Newton's so-called "Clockwork Universe". In the model of this clockwork universe, if we know the precise position and velocity of every atom in the universe at a given moment, the entire future of the universe would be apparent - it would be determined. In the clockwork universe model, the universe is just a big machine, with its gears meshing in a mechanistic manner. However, quantum theory says that nature - at its most fundamental level - is instead fired by a series of small, completely random events, and we are forbidden from "digging deeper" to find the cause of the randomness due to the limitations on our ability to obtain deeper knowledge (due to the Heisenberg Uncertainty Principle, discussed earlier in Quantum Mechanics: An Introduction).

It's as if we're all players in a game of chance at nature's Quantum Casino.

In the Quantum Casino we can imagine a roulette wheel as being a device which determine property values. When the ball comes to a rest, it is equivalent to taking a measurement of a property value: the value is the number of the slot in which the ball rests. It is clear that the choice is random, and we will see in the discussion that follows on this page that the property can only take certain allowed values (the slot values in the roulette wheel).

This random behaviour reveals something very fundamental about quantum mechanics: quantum mechanics only tells us the probabilities of a measurement outcome taking a particular value - quantum mechanics can never make an exact prediction about which value will result. This is because quantum mechanics is a statistical theory: it cannot accurately predict the outcome of a single measurement, it can only give the probabilities of outcomes when we make a series of measurements. You might think that is a major shortcoming of quantum mechanics, but actually it can be a very powerful tool to know the probability of an outcome, especially when you are dealing with millions of random events (as is the case with millions of particles). No casino knows the outcome of each spin of the roulette wheel, but casinos know that probability is on their side. And you never see a poor casino!

And the Quantum Casino is special for another reason. On a roulette wheel in a normal casino it is actually possible to predict (in theory) where the ball will land. If you can measure the precise speed that the wheel spins, and you can measure the precise speed that the croupier throws the ball, then, by using our knowledge of classical physics and Newton's Laws of Motion it is theoretically possible to work out where the ball will finish. It's not easy, but it's possible.

The Quantum Casino is different. In the Quantum Casino there is no way of calculating where the ball will land. It's as if there is a bouncer preventing you from making your measurements. You are not able to measure the speed of the wheel. You are not able to measure the speed of the ball. You are prevented from seeing that information. Similarly, in the quantum world when we are measuring a property of a particle we are fundamentally prohibited from digging deeper to analyse the quantum mechanism to try to predict the result (due to the Heisenberg Uncertainty Principle). That's a fundamental limit on physics. We just have to accept that the result of the measurement we get will be random. We can do not better. We can never do any better. This is why we have to consider the quantum behaviour of nature as being fundamentally random: because no deeper layer can ever be accessible to our analysis.

Quite bizarrely, we will also see that before we take the measurement, we have to consider the property as taking all possible values! This is equivalent to the situation when the ball is racing around the roulette wheel (i.e., before the measurement is taken), the ball could potentially come to a rest in any slot. This explains the interference effect in the double-slit experiment: before the position of the particle is detected, it must be considered as being in all possible positions.

So now we will consider how these results are derived, creating a mathematical model which enables us to calculate those quantum probabilities.

The Wavefunction

In the previous page Quantum Mechanics: An Introduction, the results of Planck and de Broglie were presented revealing that sometimes waves can act like particles, and sometimes particles can act like waves:

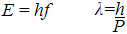
The question was posed: would it be possible to make sense of this strange wave/particle duality by combining these two results in a single equation, and in the process reveal some insights into the true nature of reality at the quantum level?

If a particle can act like a wave, this raises the question "What is the nature of the wave?" Let's consider the equation for a travelling wave:

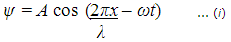
Using this formula we can construct a highly-simplified model which treats the wave associated with a particle as a travelling wave in one dimension (see here). The resulting wave is called a wavefunction, . We might imagine the wavefunction for a particle as a strange entity spreading out through the whole of space. For the double-slit experiment, we could think of this wavefunction as being the entity which passes through both slits at once, creating the interference pattern.

(Note: Equation (v) is a compact form of the Schrödinger equation. We can get the full form if we replace the energy, E, by the sum of the kinetic energy and potential energy for a particle. A full derivation of the Schrödinger equation is presented on the Cosmic Universe page.)

So in equations (iv) and (v) we see we have two different forms of the wavefunction depending on whether we wish to measure a particle's momentum or its energy (object properties which are subject to the quantum mechanism - such as position or momentum - are referred to as observables).

(The two pairs of observables in these two equations - position/momentum and energy/time are called complementary or conjugate pairs of observables because the Heisenberg Uncertainty Principle states that the more accurately we determine one observable's value in a complementary pair, the less accurately we can determine the other observable's value. For example, the more accurately we measure a particle's position, the less accurately we can measure its momentum. The energy of a particle at a certain time (energy/time) would form another similar complementary pair of observables. Every type of observable has a corresponding complementary observable. See back to the previous page on Quantum Mechanics: An Introduction for a discussion of the Heisenberg Uncertainty Principle.)

Considering the equations, each type of observable is associated with a different operator. An "operator" represents some mathematical operation. For example, for the momentum observable in equation (iv), the momentum operator on the left-hand side of the equation is a differentiation with respect to position:

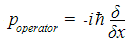
So the wavefunction equation can then be represented as:

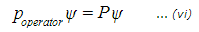
What we have here on the left-hand side of the equation is the momentum operator operating on the wavefunction, while on the right-hand side we have a scalar value for momentum (a number), P, multiplying the wavefunction. This format of equation is well-known in mathematics with the wavefunction being known as an eigenfunction and the scalar momentum value being known as an eigenvalue (for the English translation of the German "eigen", see the Comments section at the bottom of the page).

The form of the wavefunction is different depending on which observable we wish to measure. For the momentum observable measured along the x axis it can be shown that the wavefunction takes the form of a plane wave:

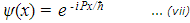
This can be demonstrated by substituting this value for into the left-hand side of the eigenvalue equation (vi), and arriving at the correct right-hand side:

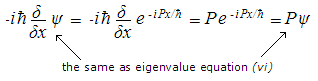
Hence the wavefunction presented in (vii) is a solution of the eigenvalue equation (vi). It can be seen that the wavefunction defined in (vii) has the form of a wave in complex space - not our everyday 3D Euclidean space. So don't make the mistake of trying to imagine the wavefunction as a simple wave in our space (as if it were a wave on the ocean). It has to be considered as a wave in complex space. The apparently esoteric mathematical field of complex numbers is now revealed as being a key element of quantum reality.

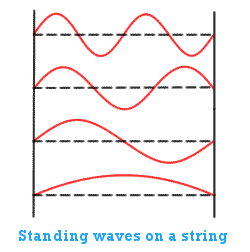
So we have shown the wavefunction to be a peculiar entity spreading out through space, but when we make a precise measurement of a particular particle's observable (such as its position) we can get a precise value. For a particle in a particular state, that value is restricted to be one of a set of possible values - one of the eigenvalues. In this sense, eigenvalues could be thought of as the only "allowed" values, with the corresponding "allowed" states being called eigenstates (the allowed values are the equivalent of the numbered slots on the roulette wheel in the Quantum Casino). This arrangement is similar to the situation of a standing wave on a string. For a particular arrangement of a string fixed at both ends only certain resonant arrangements of the wave are allowed:

State Space

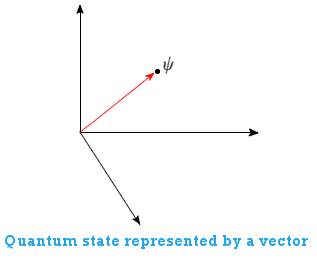
The wavefunction could be thought of as describing the value any observable of the particle before observation. In other words, the wavefunction could be thought of as the quantum state of the system. In order to analyse this behaviour of the system, it is useful to represent the wavefunction state as a single point vector in a state space:

The particular type of state space used for this representation of wavefunction state vectors is called a Hilbert space. A Hilbert space is a complex vector space (the lengths of the vectors within the space are described by complex numbers - see here). We can represent the eigenstates by orthogonal vectors called eigenvectors:

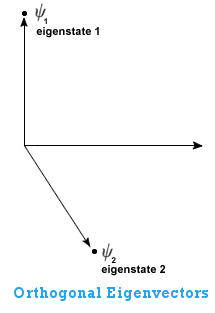
The Spectral Theorem states that these eigenvectors form an orthogonal basis which can be used to span the entire vector space. This means that whatever state the system is in (represented by the red arrow below), we can represent it as being a sum (superposition) of varying amounts of the eigenstates. The amount that each eigenstate contributes to the overall sum is called a component:

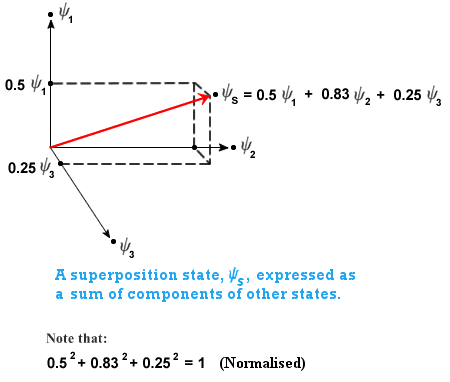
Hence any wavefunction state of the system can be generated from linear combinations of the eigenstates (this is what is known as quantum superposition). Rather remarkably, before the measurement is taken, a quantum system can exist in a mix of all of its allowed states simultaneously. This is what we see in the double-slit experiment: all of the possible position states of the electron combine to produce an interference pattern. (This is equivalent to the state when the ball is spinning around the roulette wheel in the Quantum Casino: the ball could potentially land in any slot when we take the measurement, so before we take the measurement we have to consider the system as being in a superposition of all possible states).

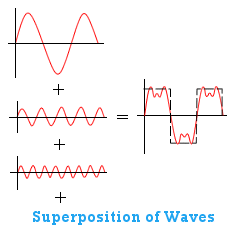
An analogy can be made with the superposition of waves. It can be shown that a complicated composite wave (representing the state vector) is composed of varying quantities of simple harmonic waves (representing the eigenstates):

The act of applying a specific operator (associated with a particular observable) therefore results in the system appearing to "jump" to a particular eigenstate, with an associated eigenvalue (equivalent to the ball coming to rest in the roulette wheel in the Quantum Casino). This is the mathematical equivalent of the process of "taking a measurement" of an observable quantity. For Hermitian operators (the type of operators encountered in quantum mechanics) the eigenvalues are always real (as opposed to imaginary). These real values represent the value of the observable that we measure when the system jumps to the corresponding eigenstate:

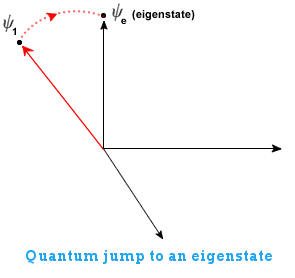
(We shall see in the page on Quantum Decoherence that this apparent "jumping" might well be just an illusion.)

At this point, the wavefunction is said to have "collapsed" to an eigenstate (this "jumping" process means we do not normally have to deal with objects in their superposition quantum states - a cat being both alive and dead at the same time, for example). Considering the analogy with wave superposition, this is the equivalent of the system picking just one simple harmonic wave out of the complicated composite wave.

If we measure the observable again we appear to get the same result - no probability involved. The wavefunction is said to have "collapsed" to a particular (eigen)value of the observable.

(Historical note: This state space representation was developed by the great British physicist and mathematician Paul Dirac. In doing so, he showed that the then-competing representations of Schrödinger's wave mechanics (we have just considered the wavefunction) and Heisenberg's matrix mechanics had the same representation in the state space and were therefore, in fact, identical.)

But to which of the many possible eigenstates does the system state appear to jump? The eigenvalue is selected on a purely probabilistic basis. Whenever we make a measurement it is as if a dice is thrown (behind the scenes) and one of the allowed states is selected at random.

All we can say is that if an eigenvalue makes a large contribution to the shape of the wavefunction, the probability of it being the selected eigenvalue is increased. The probability of a state vector jumping to a particular eigenstate is related to the dot product of the state vector and the particular eigenvector. Basically, the nearer the current state is to a particular eigenstate, the more likely it is to jump to it (which makes a lot of sense when you think about it).

This random behaviour reveals something very fundamental about quantum mechanics: quantum mechanics only tells us the probabilities of a measurement outcome taking a particular value - quantum mechanics can never make an exact prediction about which value will result. This is because quantum mechanics is a statistical theory: it cannot accurately predict the outcome of a single measurement, it can only give the probabilities of outcomes when we make a series of measurements.

Summary

Here is a useful summary of what we have discovered so far:

• Particles have characteristics called observables.
• After measurement (observation), a particle's observable can take one of several possible values called eigenvalues.
• Before measurement (observation), a particle's observable acts as though it is in a mix (superposition) of those possible eigenvalues.
• The selection of the particular eigenvalue appears to be a completely random process. Hence, quantum mechanics gives purely statistical predictions: it cannot accurately predict the outcome of a single measurement, it can only give the probabilities of outcomes when we make a series of measurements.

Bra-ket Notation

Paul Dirac developed bra-ket notation as a framework to describe quantum mechanics. A state (vector) is described by a column vector, , called a "ket". For each "ket" vector there is a corresponding row vector, , which is called a "bra". The bra is transpose of the complex conjugate of the ket vector (also called the Hermitian conjugate or adjoint).

The inner (or dot) product of the bra vector, , with the ket vector, , is denoted by:

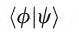
It was stated earlier that the probability of a state vector jumping to a particular eigenstate is related to the dot product of the state vector and the particular eigenvector. The probability is actually given by the square of the magnitude of the dot product. So the probability of the state jumping to the eigenstate is denoted in bra-ket notation by:

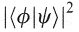
It is also possible to define an outer (or tensor) product of the ket vector, , with the bra vector, , denoted by:

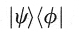
So the inner (or dot or scalar) product is:

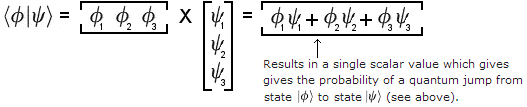
And the outer (or tensor) product is:

Back to the main page

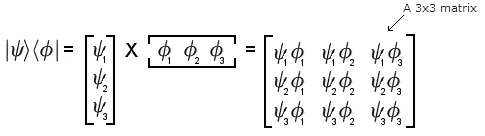
Comments

Here you can add your comments about this article.
Your comments will appear instantly on this page (underneath this form):

1) First, please enter your name:


2) Please enter your comment (max. length 3000 characters):

characters remaining

Above, you write, "So in equations (iv) and (v) we see we have two different forms of the wavefunction depending on whether we wish to measure a particle's position or its momentum." But the eigenvalues are p and E. So don't you mean you can measure the MOMENTUM or ENERGY? On the other hand, Equation (iv) is the equations for psi(x), i.e., what the wave function looks like in space. Therefore it shows where the particle might appear - it's POSITION. If that's so, then doesn't Equation (v) show it's TIME, i.e., WHEN the particle might appear? - Stan M., 19th February 2007

Between Equations (iii) and (iv) above, you use psi=Acos(). Immediately afterwards, you replace the cosine with e^(). But cos() and e^() are only equivalent if you agree to ignore the imaginary part. Doesn't this make your remarks above, that "the wavefunction defined in (vii) has the form of a wave in complex space - not our everyday 3D Euclidean space. So don't make the mistake of trying to imagine the wavefunction as a simple wave in our space" incorrect? Your own expression for the wavefunction was a cosine until you arbitrarily added in an imaginary part, turning cos() into cos() + i sin(). Right? - Stan Mohler, Jr., 19th February 2007

Thanks for your comments, Stan. I think you're right on all counts (I'm glad someone is paying attention!). Regarding your first point, I have corrected the text. Regarding your second point, Schrodinger made the great step of realising that the wavefunction should be expressed in a complex space, so the derivation moves from a plane wave with no imaginary components to a similar wave in complex space (same frequency and wavelength). I see the Wikipedia derivation of the Schrodinger equation is now very similar to the one presented here: http://en.wikipedia.org/wiki/Schrödinger_equation and that simply says: "Schrodinger's great insight, late in 1925, was to express the phase of a plane wave as a complex phase factor", so the complex nature of the wave is simply proposed as a potential solution. - Andrew Thomas, 19th February 2007

Under "Bra-ket notation" you you say that the ket is a row vector. I believe in standard notation the ket is a column vector and the bra a row vector. However under your inner and outer product definitions you DO show the ket as a column vector!
You are doing a great job making all this information available on the Internet. - Les hawker, 11th March 2007

Thanks for the compliment and spotting the error. I'm glad people are looking! I've corrected the text. - Andrew Thomas, 11th March 2007

'eigen' is not German for 'certain'. It means something more like 'personal' or 'idiosyncratic', or 'own'. Given that the concept was around long before QM, there's no reason to expect it to mean something related to what it happens to represent in QM.

A mirror-image translation, where English replaces the German and German the English, is often given as 'characteristicwert'. - arc, 27th March 2007

Very interesting, thanks for that information. I'll modify the text. - Andrew Thomas, 28th March 2007

As usually happens on the 'net, I stumbled upon your brilliant site by asking a frivolous question "Can waves be used to predict random events?". Not that I was expecting a revelation. In fact, as layman, I was hoping to be led to some fundamental properties of "randomness". I haven't finished reading all the articles but in "The Quantum Casino" article I found all that I needed to know and I quote "..we are forbidden from "digging deeper" to find the cause of the randomness due to the limitations on our ability to obtain deeper knowledge..". Unquote. So until such a time as we have "deep" knowledge, no one will be able to predict the future. That time may be tomorrow or in a million years. Sorry if I sound apocalyptic but I believe it will be possible one day. - Bowie Muyutu, 5th December 2007

Thanks, Bowie. Yes, it appears there are fundamental limitations on our ability to predict the future. And we may NEVER be able to overcome that. - Andrew Thomas, 5th December 2007