Quantum Entanglement
Part 3 of "An Introduction to Quantum Reality"
It is possible for a particle to interact with another particle in such a way that the quantum states of the two particles form a single entangled state. The definition of an entangled state is that it is not entirely independent of other states: its state is dependent on another state in some way. Because of this dependency it is a mistake to consider either state in isolation from the other. Rather we should combine the states and treat the result as a single, entangled state.
For example, a light beam is a composed of a stream of photons. The direction of light's electric field is its direction of polarization. The polarization direction of a photon can be at any particular angle, for example "vertical" or "horizontal". It is possible to generate a pair of entangled photons if, for example, a laser is shone at a crystal. In that case a single photon can split to become two photons. Each photon produced in this way will always have a polarization orthogonal to the other photon (see this Physics World article or this Laser Focus World article). For example, if one photon has vertical polarization then the other photon must have horizontal polarization (this is due to the law of the conservation of angular momentum: angular momentum of the system before the split must equal the angular momentum of the system after the split).
So if two people each receive one of the entangled photons and performs a measurement, they will find that the other person's photon has orthogonal polarization. There is an apparent connection between the particles, no matter how far apart they are taken (see this interview with Anton Zeilinger about "spooky action").

"I cannot seriously believe in quantum theory because it cannot be reconciled with the idea that physics should represent a reality in time and space, free from spooky actions at a distance." - Albert Einstein
The EPR Paradox
Einstein was never happy with the implications of quantum theory and at the legendary 1927 Solvay conference (and throughout the late 1920s) he proposed several thought experiments which he believed revealed flaws in the theory. However, all of these objections were successfully refuted by Niels Bohr, and a humbled Einstein went home to lick his wounds. However, in 1935 Einstein and two colleagues, Boris Podolsky and Nathan Rosen (EPR) described a thought experiment commonly referred-to as the EPR paradox, the implications of which shook quantum theory to its core.
Einstein's great objection to quantum theory came from its denial of physical reality before observation (quantum theory says that only after we measure a property value of a particle does that property gain physical reality - before we measure it we must consider it to be in a superposition state). We often quote Einstein's rejection of quantum indeterminacy: "God does not play dice", but his less-quoted objection to quantum theory's denial of physical reality reveals his more serious concern: "I like to think the moon is there even if I am not looking at it."
In order to dispute quantum theory on this basis, the EPR paper contained - for the first time in the history of science - an operational definition of physical reality:
"If, without in any way disturbing a system, we can predict with certainty the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity."
- Definition of physical reality from the EPR paper.
Let's say the same thing in other words: If a physical property of an object can be known without it being observed, then that property could not have been created by observation. If it wasn't created by observation, it must have existed as a physical reality before its observation.
Einstein believed that quantum entanglement could be used to reveal a flaw in quantum theory, because he thought that quantum entanglement could determine physical reality before observation - at odds with the principles of quantum theory. Consider two entangled photons, one of which is sent to observer Alice, and the other is sent to observer Bob (see the diagram below). The two observers could be a considerable distance apart. Now remember from the discussion at the top of this page that two entangled photons must have orthogonal polarizations. So when Alice measures the polarization of her photon and finds it to be, say, vertically polarized we instantly know that Bob's photon will have horizontal polarization - even though Bob has not yet measured it!
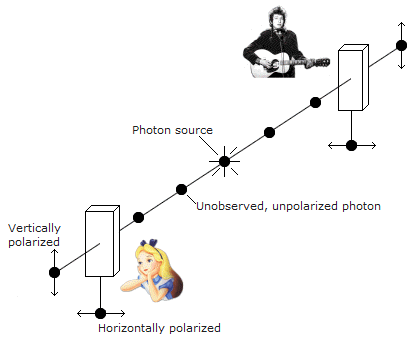
But quantum theory says that before Bob measures his photon it can have no defined value for its polarization property - it is in a superposition state. Only when Bob measures it does its value become physically real. How then can we know the result Bob will obtain before Bob measures it? The solution according to quantum theory is that it is the measurement of Alice which collapses the wavefunction of both Alice's and Bob's photons. It is the observation of the polarization of one of the photons as being, say, vertical that instantaneously collapses both photons, resulting in Bob's photon having horizontal polarization.
However, Einstein realised that such instantaneous communication of polarization value between the two photons was forbidden by his own theory of Special Relativity (nothing travels faster than light). Hence, Einstein believed that the model of quantum mechanics was incomplete: it did not describe the physical reality of Bob's photon before observation.
Einstein believed the correct way out of this paradox was to assume that Bob's photon (and all particles) possessed some sort of fixed properties which were hidden from our view (generally referred-to as hidden variables). No faster-than-light communication is then required: the particle properties were set when the particles were created. Crucially, though, this would mean the particles possessing more information than quantum theory said they should have. If particles had these hidden variables then quantum theory was wrong.
An associate of Bohr tells that "this onslaught came down upon us like a bolt from the blue. Its effect on Bohr was remarkable ... as soon as Bohr heard my report of Einstein's argument, everything else was abandoned."
Bell's Inequality
In 1964, John Bell devised an ingenious test for the existence of hidden variables. Bell's theorem (which is commonly called Bell's Inequality) has been called "the most profound discovery of science" (see here).
Bell showed that for a group of objects with fixed properties A, B and C, the number of objects which have property A but not property B plus the number of objects which have property B but not property C is greater than or equal to the number of objects which have property A but not property C.
This can be written more compactly as:
Number(A, not B) + Number(B, not C) >= Number(A, not C)
An easy-to-understand version of this inequality is provided by David M. Harrison of the University of Toronto (see here). Let's consider our collection of objects with fixed properties to be a collection of people. And let their fixed properties be the following:
- A: Sex ("Male" or "Female")
- B: Height (over 5' 6" ("Tall") or under 5' 6" ("Short" - don't be offended!))
- C: Eye colour ("Blue" or "Green")
Then, no matter which group of people you are dealing with, you are always able to issue the following statement (inequality): "The number of short males plus the number of tall people, male and female, with green eyes will always be greater than or equal to the number of males with green eyes. I absolutely guarantee that for any collection of people this will turn out to be true."
That's always true. Isn't that amazing? That's a bit of quantum mechanics you can try out at your next party!
It's relatively simple to prove this. Note that every person can be classified into one of the following eight groups:
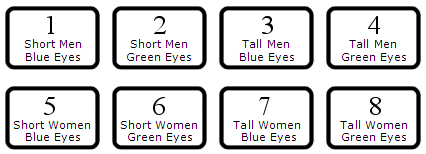
Referring to this diagram, Bell's Inequality is saying that:
(Group 1 + Group 2) + (Group 4 + Group 8) >= (Group 2 + Group 4)
Which, if you study it, is clearly always going to be true.
So Bell's Inequality will always hold true for normal, everyday objects with fixed properties. But now let's analyse the situation for quantum particles (in which case, the fixed properties would represent the hidden variables). The first thing we realise is that we've got a problem because we can no longer measure all three properties of our particle at the same time (due to the Uncertainty Principle). However, we can get round this restriction by measuring the properties of two entangled particles.
Referring back to our original statement of Bell's Inequality:
Number(A, not B) + Number(B, not C) >= Number(A, not C)
We will have to divide our quantum particles into three groups (called ensembles), and extract entangled pairs of particles from each group:
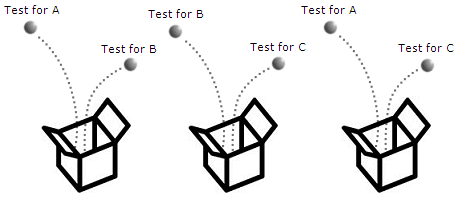
Because we cannot measure all the properties of each particle (i.e., we cannot measure A, B, and C for each particle - we can only know the values of two of the properties), we cannot conclusively say if the inequality is broken or not. The best we can do is run the test on an ensemble of many thousands of particles and consider the statistics of the results. The first published experiment was by Clauser, Horne, Shimony and Holt in 1969 using photon pairs (with the properties A, B, and C corresponding to photon polarization of 0, 45, and 90 degrees) and it was found that the statistics strongly suggested that the inequality was, indeed, violated.
What does this mean? Well, taking our example given earlier of a collection of people, considering the right-hand side of that inequality, in order for the inequality to be violated a person would have to be more likely to have green eyes if the other (entangled) person had been found to be a male. In other words, the property measurement was dependent on the type of observation performed on the other entangled particle: there is an instantaneous connectedness between the particles. What happens to one particle can instantaneously affect the other.
Summary
To sum up, Einstein believed the following:
- There was no "spooky action-at-a-distance" which apparently violated Special Relativity (i.e., there was locality).
- Objects had definite reality, properties independent of observation.
However, the violation of Bell's Inequality reveals that the reverse is true:
- There is a strange connection between particles which instantaneously informs the undisturbed particle of the type of measurement just carried out on its partner (however Special Relativity is not violated because no information can be transmitted using this method).
The implications of this result will be considered further in the later page on Quantum Reality.
The Leggett Inequality
So Einstein believed in a theory in which particles had pre-existing hidden properties independent of measurement ("realism"), and there was no "spooky" action at a distance (i.e., there was "locality"). But the violation of Bell's Inequality showed there was, indeed, some form of spooky action-at-a-distance (i.e., there was non-locality). However, it did not go so far as to prohibit the possibility of some form of pre-existing hidden variables in particles (realism).
However, in 2003 Anthony Leggett devised an new inequality which - if experimentally violated in the same way as Bell's Inequality - would invalidate the possibility of hidden variables, showing that particles could not possess "realism" in the conventional sense. So Einstein's twin principles of locality and realism would both be shown to be violated.
Leggett's Inequality is based on the fact that if we have two numbers - A and B - which can both take the values of +1 or -1 then the following is always true:
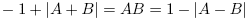
(We could, for example, consider the +1 and -1 values as representing photon polarization either up (+1) or down (-1) for two particles, A and B).
It is easy to see that this is true just by setting A and B to either +1 or -1 and examining the four possible situations:
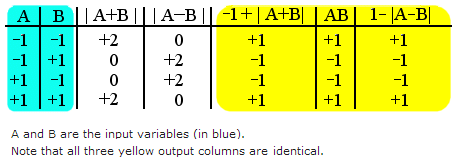
The inequality based on this principle was recently tested experimentally and, indeed, found to be violated (see arXiv paper quant-ph/0704.2529v1 for details of the experiment and a description of Leggett's Inequality, also see this Physics World article or this New Scientist article). So it would appear that Einstein's twin pillars of realism and locality both come crumbling down.
(However, in the page on Quantum Reality we will see that it might be possible to consider the quantum superposition state as "reality before observation". In that case, what Leggett's Inequality reveals is that "reality before observation" - our A and B photons above - cannot be a clear-cut +1 or -1 form (for example, photon polarization up or down). Instead, any reality would have to be a superposition mix of the two values: +1 and -1. This eliminates most conventional views of realism. However, we already knew from experimental results such as interference effects in the double-slit experiment that particles behave as though they are in a strange quantum superposition state before observation, so I'm not sure this tells us anything new. Any "reality before observation" would have to be a rather peculiar "multi-valued" reality, and Leggett's Inequality would not appear to eliminate pre-existing reality of this form (for more on multi-valued reality see the section "Beyond Copenhagen" on the Quantum Reality page).
Qubits
The secret for analysing entangled systems is that you can no longer talk of the wavefunction for just a single localised particle, you have to to talk of one single wavefunction for the entire system.
It's quite useful at this point to introduce
another useful piece of common notation. In the previous page on The Quantum
Casino we were introduced to the common "bra-ket" notation, with a state
being denoted by 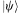 . If we have two states,
. If we have two states,
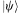 and
and 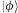 , then the joint state is
the tensor product of the two states (see back to the explanation of the tensor
product in The Quantum
Casino). The resultant, single state is then:
, then the joint state is
the tensor product of the two states (see back to the explanation of the tensor
product in The Quantum
Casino). The resultant, single state is then:
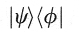
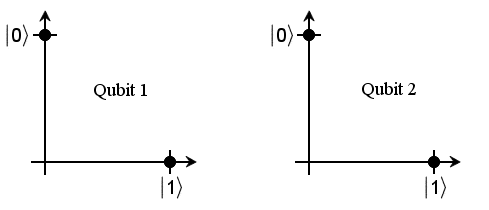
For an example, consider a particle which, after measurement, can be in one
of two states: 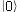 or
or 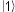 (a particle such as
this is known as a Qubit and is used in the exciting new field of Quantum
Computing). The orthonormal basis of the Hilbert state space should
therefore have two vectors representing the
(a particle such as
this is known as a Qubit and is used in the exciting new field of Quantum
Computing). The orthonormal basis of the Hilbert state space should
therefore have two vectors representing the 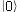 and
and 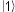 states (a
two-dimensional Hilbert space is denoted by H2 - see
back to the page on The Quantum
Casino for an explanation of Hilbert spaces and the orthonormal
basis):
states (a
two-dimensional Hilbert space is denoted by H2 - see
back to the page on The Quantum
Casino for an explanation of Hilbert spaces and the orthonormal
basis):
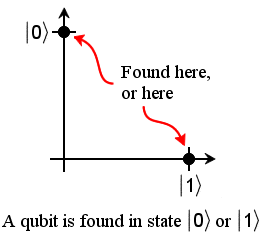
Before measurement, and "wavefunction collapse", the qubit's state could be
any mix (superposition) of these two states. But after measurement, the qubit's
state is always found to be in state 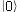 or
or 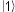 (the superpositions
apparently disappear).
(the superpositions
apparently disappear).
What happens if our qubit is a photon and has an entangled partner photon (as explained earlier)? You might think each photon has its own state, and hence each photon would have its own separate Hilbert state space:
That's wrong.
Remember that the states of two entangled photons are dependent on each
other. For our entangled qubits, let's say that if the first qubit is in state
![]() then the second qubit is constrained to be in state
then the second qubit is constrained to be in state 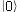 as well, and if the
first qubit is in state
as well, and if the
first qubit is in state 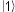 then the second
entangled qubit is constrained to be in state
then the second
entangled qubit is constrained to be in state  as well. Now instead of
having two separate state spaces for the two qubits we have one
entangled state space, and instead of one wavefunction for each qubit
we now have one wavefunction for the entire system (composed of
two qubits).
as well. Now instead of
having two separate state spaces for the two qubits we have one
entangled state space, and instead of one wavefunction for each qubit
we now have one wavefunction for the entire system (composed of
two qubits).
In order to construct the entangled space, we first see that each of the two vector spaces is spanned by similar sets of two basis vectors:
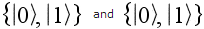
The resultant single, joint state space can be constructed by taking the tensor product of the two sets of basis vectors of the two original state spaces (the tensor product of two vectors is a matrix - see back to the discussion of bra-ket notation in The Quantum Casino). This is achieved by performing a matrix multiplication of the two sets of basis vectors:
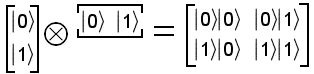
We can see that the original two-dimensional state spaces combine to produce a single four-dimensional state space:
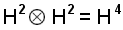
So the resultant set of four basis vectors for the new entangled space is:
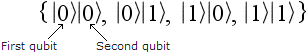
Note that with just one entanglement the Hilbert space has rapidly increased from two dimensions to four dimensions. This rapid increase in the dimensions of the Hilbert space due to entanglement will be shown to be key to what really happens during "wavefunction collapse". This will be explained in the next page on Quantum Decoherence.
For more on qubits and this method, see this PowerPoint presentation.
Separable and Entangled Systems
After receiving the comments of AKP below, I decided it would be useful to clarify the distinction between separable and entangled systems.
Let's consider eye colour (which can be either blue or green) of two non-related people. The two people could be treated as a single system, in which case the resultant combined system (I see Wikipedia call it a composite system here) could have four possible states for eye colour (essentially, each person is like a qubit, and we are dealing with a two-qubit system):
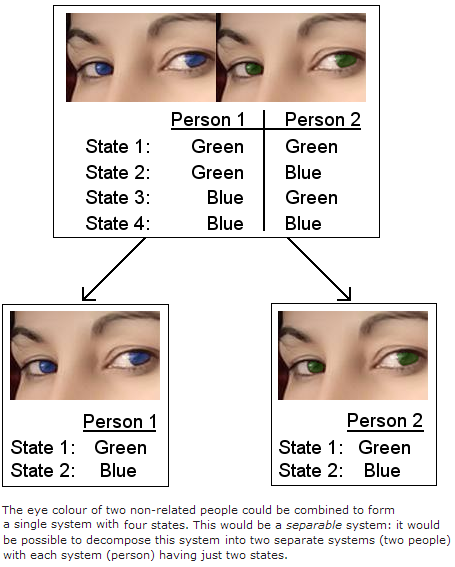
It is possible to decompose the system because there was no dependence between the eye colour of person 1 and the eye colour of person 2: they were completely independent systems. However, if we now consider the situation of identical twins we find there is now a dependence: the eye colour of person 1 depends on the eye colour of person 2 - they are identical.
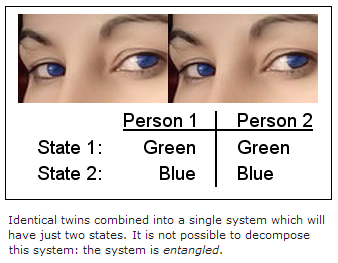
It is now not possible to decompose this system into two separate systems (people) because of that dependence between the two twins. For example, you are no longer free to select blue eyes for person 1 and green eyes for person 2 - that combined state is forbidden. For this reason, this combined system with the two twins is non-separable: it is an entangled state. So this is the reason why an entangled two-qubit system cannot be decomposed into two independent one-qubit systems.
For a mathematical description of this, see the PowerPoint
presentation, especially pages 16-20 on "Two Qubits". On page 20, "Two
Qubits, Entangled", you could think of the 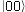 entangled state
as representing the situation when both identical twins have blue eyes, and the
entangled state
as representing the situation when both identical twins have blue eyes, and the
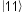 entangled state as
representing the situation when they both have green eyes.
entangled state as
representing the situation when they both have green eyes.
Comments
Here you can add your comments about this
article.
Your comments will appear instantly on this page (underneath this
form):
Many thanks for this site. I have been looking for something like this for ages. I want to understand QM, but getting past the basic concepts and jargon on for example wikipedia was proving too laborious. These pages you have created a real blessing. - Frank, 25th February 2007
Thank you so much, Frank. That's appreciated. I tried to make it as readable as possible. - Andrew Thomas, 25th February 2007
nice page! i'll be sure to come
back to read more. a few questions/comments to possibly consider:
maybe
you could expand the heisenberg uncertainty comments into a paragraph. i think
its important to talk about the difference between two conjugate measurements on
one particle and these measurements being performed on separate particles from
the same ensemble. and being a statement about standard deviations in
measurements on two different groups of particles, the principle is not telling
us how one measurement will "disturb" the results of a second conjugate
measurement.
regarding particle spin measurements, if i have an ensemble
of x-spin-up particles and i measure y-spin and z-spin each on a half of the
ensemble, dont i get 1/2, 1/2 in each case? isnt this perfectly precise? what is
lower bounded here is the product of the std devs of these two probability
distributions. again being measurements on different particles.
i really
liked the clarity of the bell inequality discussion. it would be cool to see a
picture like the green eyes, etc. with the quantum tests inserted.
jmahoneyatphysicsdotucdavisdotedu - john, 29th March 2007
Hi John, thanks for your
comments. I've actually just added a section on the Heisenberg Uncertainty
Principle to my page "Quantum Mechanics: An Introduction": http://www.ipod.org.uk/reality/reality_quantum_intro.asp
Regarding your comments about particle spin, I'm really referring to
what might be called a "generalized Uncertainty Principle" - not the same as the
complementary pair idea (see http://en.wikipedia.org/wiki/Spin-1/2
). This just states that you can't measure all spin values simultaneously:
taking a measurement along one axis destroys the information in the other axes.
- Andrew Thomas, 30th March
2007
This is an excellent resource for those who only want to understand instead of being bombarded with intense mathematics and obscure terminology. If only more scientists would write like the author of this page. Very much appreciated. - Gibran Shah, 9th May 2007
Thanks very much, Gibran. I'm trying to strike a happy medium by making the articles accessible to the general reader, but also providing more advanced technical information and mathematics for those who want to dig a bit deeper. - Andrew Thomas, 9th May 2007
Hi Andy, Excellent site! I
think it's fantastic that you're presenting QM fundamentals in such an easy to
understand manner. I do have a question about your phrasing, though. In my
experience, two particles are said to be "entangled" iff their joint state is
not decomposable as a tensor product of two individual states. So it's a bit
confusing to read your explanation here:
"then the entangled state is
the tensor product of the two states (see back to the explanation of the tensor
product in The Wavefunction). The resultant, single entangled state is then..."
Perhaps you mean "the composite state" or similar instead of "entangled
state"? Keep up the good work! - AKP, 16th June
2007
Hi AKP, thanks for your
comments. I've added an entirely new section to the main text - "Separable and
Entangled Systems" - because of your comments to clarify the situation. You're
right, two systems are said to be "entangled" if their joint state is not
decomposable as a tensor product of two individual states - this would be the
example I give of the eye colour of two identical twins. You can't decompose the
system into two independent people because of the dependency. It's an entangled
system.
But you're right - I shouldn't have described the entangled
state space as resulting from the tensor product of the two state spaces. I've
changed the wording to "joint state space" instead of "entangled state space".
Thanks. - Andrew Thomas, 18th June
2007
Above you have:-
Number(A,
not B) + Number(B, not C) >= Number(A, not C)
with C:Eye colour ("Blue"
or "Green") but "not C" is "not Blue" rather than "Green" as you have it later.
Blue and green are not the only eye colours.
B: Height (over 5' 6"
("Tall") or under 5' 6" ("Short")) is OK since it covers everyone
A: Sex
("Male" or "Female") could also be dubious. - John Middlemas, 22nd July 2007
I suppose you have a point about the eyes - but surely everyone falls into one of the two sex categories! - Andrew Thomas, 22nd July 2007
Nice but..... what is actually
entangling these particles? How are they actually linked. Maybe the
superposition is forced to randomly collapse in a way that however maintains the
conservation of energy, so that it sums up to zero.... is that enough to explain
it? Or do you need communication for the particles to know how to maintain the
conservation of energy? And if so... HOW!
- Morn, 12th September 2007
Well, nobody knows the answer to that. If you know, please tell us!! David Bohm tried to explain it by his "Implicate Order" idea which proposed the universe had a hidden holistic connectedness - see the blue box on "Hidden Variables Theories" on the Quantum Reality page: http://www.ipod.org.uk/reality/reality_quantum_reality.asp You might also want to look at the next section on that page which describes the related idea for some sort of instantaneous communication within a "veiled reality" layer: "The hidden variables mechanism in the veiled reality layer transmit the characteristics between the particles instantaneously. However, we are always fundamentally incapable of accessing those hidden variables in that veiled reality." - Andrew Thomas, 12th September 2007
Hi Andrew, it is interesting that uncertainty relation arises between two orthogonal components of the angular momentum (not between two orthogonal components of the momentum); the momentum acts like an unitary observable, but the angular momentum acts like three separate observables! - Marian, 29th September 2007
Hi Marian, yes, that's very interesting. It's another example of how we have to be careful not to confuse intuitive classical concepts in physics with quantum mechanical concepts. (For the technically minded, Wikipedia shows how the components of angular momentum do not commute, i.e., the result we get when we measure two components depends on the order in which we measure them - hence the Heisenberg Uncertainty Principle kicks in: http://tinyurl.com/2dg52r ) - Andrew Thomas, 29th September 2007
I was confused by your statement "Bell showed that for a group of objects with fixed properties A, B and C, the number of objects which have property A but not property B....." and wondered if you could clarify. Surely all objects must always have properties A, B, or C. It is the values of these properties which can vary? So having property A and not B, what does that mean in terms of the values? - Brett Wilson, 30th September 2007
Yes, I was a bit casual in the
use of "properties" and "values". The way it is written is such that instead of
property A being "Sex" with two possible values - "male" or "female" - I'm in
fact defining property A as "maleness" with two possible boolean values: "true"
or "false". Similarly, instead of property B being "height" with two possible
values - "tall" or "short" - I'm in fact defining property B to be "tallness"
with the same two possible boolean values: "true" or "false".
So if
property A is "true" we're actually saying it's a male, and if property A is
"false" then it's a female. And when I say "The number of objects which have
property A (i.e., property A is true) but not property B" I mean the number of
short males.
If instead we consider the "The number of objects which do
NOT have property A but DO have property B" it would be the number of tall
women. I hope that's clarified what I meant in the text (or maybe not!). -
Andrew Thomas, 30th September
2007
Hi. This is the best site I have come across which explains complex ideas in everyday language. If you are not a professor, then you sure should be. A shortcut to this one will be on my desktop, you can bet! - Bruce Penney, 25th October 2007
Oh, you're too kind! - Andrew Thomas, 25th October 2007
