Quantum Decoherence
Part 4 of "An Introduction to Quantum Reality"
Hopefully by this stage you will have read the previous pages on Quantum Mechanics: An Introduction, The Quantum Casino, and Quantum Entanglement. On those pages several weird and puzzling questions were raised. In this page we start to see some answers.
Perhaps the first principle to understand is the idea that we cannot separate an object being measured (observed) from the apparatus performing the measurement. This is clearly shown in the quantum world where you cannot divorce the property you are trying to measure from the type of observation you make: the property is dependent on the measurement.
It's actually quite like a rainbow. When a person looks at a rainbow he sees it starting in a certain position and ending in a certain position. However, when a second person - who is standing in another place - looks at the rainbow he will see it starting and ending in a completely different spot. So the two people are effectively seeing different rainbows, with different starting and ending positions. That's why you will never find a pot of gold at the end of a rainbow!

How is this possible? It's possible because you have to consider the rainbow and the observer as a single system. Actually, this is true of all measurements and observations: you really cannot separate the object being measured from the device performing the measurement or observation - you have to consider them as a single system. For example, when you take the temperature of an object using a thermometer, you have to remove a very small sample of heat from the object. The measuring device has altered the object - the two entities are not separate. The object and the device performing the measurement are bound together as a single system.
This idea of the observed object and the observer being bound together as a single system will be shown to be the key to providing the mechanism for the apparent "collapse of the wavefunction". Because, in reality, a quantum particle is rarely completely isolated from its environment. Rather, the particle and the environment are bound together as one system.
How the environment eliminates interference effects
In the page on The Quantum Casino we have seen that when a measurement of an observable is performed, the quantum state appears to "jump" to a particular eigenstate (with the observable taking the associated eigenvalue). This apparent jumping puzzled physicists for many years because it was not understood how and why the usually linear time-evolution of the Schrödinger equation should suddenly decide to make a sudden jump.
Also, as a quantum state can be viewed as a superposition of many other states, the question can also be asked as to why we never see these other states in macroscopic objects. For example, why is Schrödinger's cat never seen as being both alive and dead at the same time?
However, in the double-slit experiment we do see the other states of the superposition, as they provide constructive and destructive interference effects (see Quantum Mechanics: An Introduction). Why do these so-called interference states appear in the double-slit experiment but apparently vanish in macroscopic objects?
Let's remind ourselves of how a quantum state can be expressed as a linear combination of components of other eigenstates (this was considered in the page on The Quantum Casino):
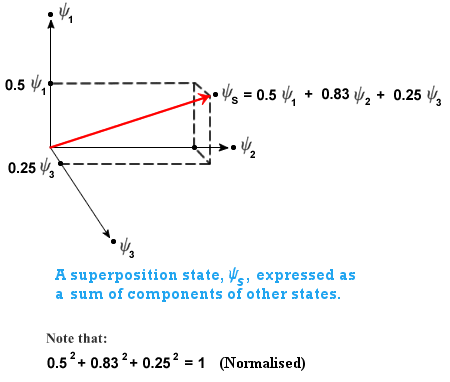
Now here is the absolutely key point: every component eigenstate has an associated phase (this was considered back in The Quantum Casino). It is this phase which gives the wavefunction its "wavelike" character (in complex space, remember). In order for the components to combine together correctly to produce a superposition state, they must be in the same phase (must be coherent). This is what happens in the double-slit experiment: interference components possessing the same phase combine to produce the interference effects.
As explained in the "rainbow" example at the top of this page, we cannot separate an observed object from the observer: we have to treat the resultant combined system as one system. What happens in the real world is that a particle is not perfectly isolated: a particle inevitably interacts with the environment. These interactions have the effect of the particle "being observed" by the environment - the "environment" might very well be a man-made measuring device, for example. (For a technical discussion about the measured system and the measuring apparatus acting as one system, see here. For more on the idea of environmental interactions producing a measurement, see the page on Quantum Reality).
What happens to a quantum particle in the real world is that each of its component states gets entangled (separately) with different aspects of its environment. As seen in the page on Quantum Entanglement, when particles become entangled you have to consider them as one single, entangled state (you use the tensor product to calculate the resultant state). So each component of our quantum particle forms separate entangled states. The phases of these states will be altered. This destroys the coherent phase relationships between the components. The components are said to decohere.
If a particle interacts with just a single photon, for example, then the two particles will enter an entangled state and that will be enough to trigger the onset of decoherence (for example a single photon entering the double-slit experiment will be enough to destroy the interference pattern). However, for all interference effects to disappear, the particle must have a macroscopic (rather than a microscopic) effect by forming entanglements with billions of particles in, say, a Geiger counter. This is described in the book Quantum Enigma: "Whenever any property of a microscopic object affects a macroscopic object, that property is 'observed' and becomes a physical reality" (this idea of "decoherence=observation" is considered in greater detail in the next page on Quantum Reality). In that case, if there are no longer any interference terms then to all intents and purposes the particle is now in a single, quantum state - one of the component eigenstates:
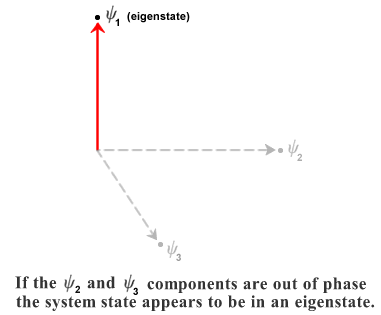
(In the page on Quantum Entanglement it was shown how the dimensionality of the Hilbert state space increases rapidly with each entanglement, thus further reducing the chance of coherent interference effects - see here)
Note that the interference components do not actually disappear - because they are out of phase we just don't notice them at the macroscopic level. In fact, they just get dissipated out into the wider environment. I always imagine them as little ripples in the ocean - we only ever notice the big (macroscopic) waves in the ocean. The little ripples get entangled with other little ripples until it is impossible to tell from which big wave each little ripple came.
Imagine you throw a rock in the sea off the coast of the United Kingdom. After the initial big splash, the ripples dissipate and apparently disappear. But of course, they haven't really disappeared. The ripples have decreased in size, and they have mixed and interfered with other waves, but they have not disappeared. Two weeks later, on the rocky shore of Tierra del Fuego off the Argentinian coast, one of the small waves washing to shore is maybe an imperceptible fraction of one micron higher because of that rock you threw.

So the ripples (interference terms) do not actually disappear. They dissipate into the environment and become effectively undetectable. And it's certainly not possible to associate the microscopic change in the height of the wave in Tierra del Fuego with the rock you threw - there have been so many interactions with other waves along the way. In this sense, the process of decoherence is irreversible - and that's a key feature of decoherence: we can't reverse the process (to regenerate the initial interference components) - they're gone for good. And even the "little ripple" echoes of the interference effects have become imperceptible due to interactions with the environment. Then, for all intents and purposes, the interference effects (ripples) have completely disappeared.
At last we seem to have found the mechanism behind the disappearance of the interference effects, the truth behind the mysterious "collapse of the wavefunction".
Decoherence, then, is not a sudden "jumping" effect. Rather, the interference terms disappear due to the progressive influence of billions of particles (and associated entanglements) as a particle passes through our measuring apparatus. So there is a progressive filtering (of the interference terms) and amplification (of the eventual measurement - Bohr referred to an "irreversible act of amplification"). However, the decoherence process fooled physicists for many years because it is such an efficient process - decoherence happens so fast (in the region of 10-27 seconds!) - giving a false impression of a discontinuous, instantaneous quantum "jump". However, recent experiments have managed to delay decoherence by decoupling quantum particles from their environment. If decoherence is delayed then the superposition states become evident. As an example, an electric current has been made to flow in opposite directions at the same time by using a superconducting ring (see this Physics World article which considers the effect of decoherence on Schrödinger's cat, and this New Scientist article).
The reason we never see Schrödinger's cat both dead and alive at the same time is because decoherence takes place within the box long before we open it. This is due to the device housing the radioactive nucleus and the poison. This is what forms the macroscopic environment immediately surrounding the radioactive nucleus.
So why does the electron in the double-slit experiment still show interference effects? Why does it not decohere? The answer is because it is not a macroscopic object, it is an isolated microscopic object. While decoherence happens extraordinarily fast for macroscopic objects, for an electron the decoherence time (the so-called coefficient fluctuation time) is about 107 seconds, or about a year - plenty of time to perform the double-slit experiment and see interference effects.
Decoherence and the Many-Worlds Interpretation
The so-called "quantum measurement problem" has baffled physicists ever since quantum mechanics was first discovered: What constitutes a measurement? What random process selects the observed value from the possible values in the superposition? What happens to the other terms in the superposition?
In 1957, Hugh Everett proposed the many-worlds interpretation (MWI) of quantum mechanics in an attempt to provide an answer to the quantum measurement problem. The MWI suggests that when we make a measurement, the universe itself splits into different parallel universes, each universe containing one possible outcome of the observation. For example, in the case of Schrödinger's cat, when we open the box the universe splits into two: the cat is alive in one universe, and dead in the other.
I believe that recent results in quantum decoherence have given us new insights into the quantum measurement problem, and there is no longer any need to propose anything as drastic as parallel universes to explain the process. As was explained previously on this page, interference terms get dissipated out into the wider environment and become effectively undetectable. We do not need to propose that they teleport into a parallel universe - the terms remain firmly in this universe.
As was explained in the main text, there is now experimental support for this decoherence viewpoint. If particles can be isolated from the environment we can manage to view multiple interference superposition terms as a physical reality in this universe. For example, the electric current being made to flow in opposite directions (see this Physics World article, which also explains Schrödinger's cat in terms of decoherence), or the research at NIST which has created an atom in two places at the same time (see this excerpt from Jim Al-Khalili's Quantum here, or see this press release from NIST). If the interference terms had really escaped to a parallel universe then we should never be able to observe them both as physical reality in this universe.
Decoherence in an Ensemble of Particles
So decoherence solves the mystery of apparent wavefunction collapse, and also explains why we do not see superposition states in macroscopic objects, but it does not explain which particular eigenstate is selected during the "measurement" process. As explained in the page on The Quantum Casino, the selection of a particular eigenstate is governed by a purely probabilistic process, so in order to analyse this probabilistic behaviour we should consider a number of quantum particles in a similar state (called an ensemble), and then we can use a useful statistical tool called a density matrix.
Let us consider a ensemble of particles in a box. The whole box can then be treated as a single quantum system. When we extract a particle from the box and measure it we find it to be either "blue" or "green", say. Before measurement, this system can then be in one of two states (see this paper by John Boccio):
- A pure state - each of the particles is in the same state with the same state vector. For example, let's suppose all the particles in our are in the same superposition state before measuring, an equal superposition of blue and green.
- A mixed state - the particles are all in different classical states, i.e., the particles are all either blue or green: no particles are in superposition states. This is just a classical mix of blue and green particles.
When we extract particles from the box one-by-one and measure each particle to determine if it is "blue" or "green" we find that, in both the case of the pure state and the mixed state, 50% of the particles measure as "blue" and 50% of the particles measure as "green". So, after measurement, the two quantum systems appear to be identical. However, the states of the two systems before measurement were clearly different: the pure state could be described by a single state vector (all of the particles were in the same superposition state). The mixed state, on the other hand, could not be described by a single state vector (because the particles were not all in the same state: some were green, some were blue). The statistical properties of both systems before measurement, however, could be described by a density matrix. So for an ensemble system such as this the density matrix is a better representation of the state of the system than the state vector.
So how do we calculate the density matrix? Let's
imagine we have a number of qubits in a box (these can take the value
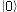 or
or 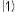 , see the page on Quantum
Entanglement). Let's say all the qubits are in the following superposition
state:
, see the page on Quantum
Entanglement). Let's say all the qubits are in the following superposition
state:
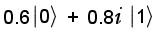
In other words, the ensemble system is in a pure state, with all of the
particles in an identical quantum superposition of states 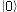 and
and 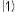 .
.
This state can be written as a column ("ket") vector (see back to the page on The Quantum Casino for a discussion of bra-ket notation). Note the imaginary component (the expansion coefficients are in general complex numbers):
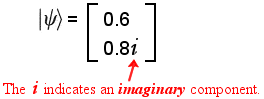
In order to generate the density matrix we need to use the Hermitian
conjugate (or adjoint) of this column vector (the transpose of the
complex conjugate of 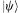 ). So in this case the
adjoint is the following row ("bra") vector:
). So in this case the
adjoint is the following row ("bra") vector:
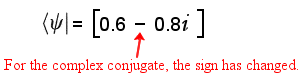
The density matrix is defined as the weighted sum of the tensor products over all the different states (see the page on The Quantum Casino for a description of the tensor product, also see here for more details):
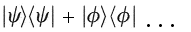
So, in this case, we can calculate the density matrix defined as the single tensor product:
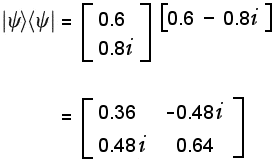
What does this density matrix tell us about the statistical properties of our
pure state ensemble quantum system? For a start, the diagonal elements tell us
the probabilities of finding the particle in the 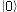 or
or 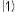 eigenstate. For example,
the 0.36 component informs us that there will be a 36% probability of the
particle being found in the
eigenstate. For example,
the 0.36 component informs us that there will be a 36% probability of the
particle being found in the 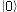 state after
measurement. Of course, that leaves a 64% chance that the particle will be found
in the
state after
measurement. Of course, that leaves a 64% chance that the particle will be found
in the 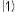 state (the 0.64
component).
state (the 0.64
component).

The way the density matrix is calculated, the diagonal elements can never have imaginary components (this is similar to the way the eigenvalues are always real - see back to the page on The Quantum Casino). However, the off-diagonal terms can have imaginary components (as shown in the above example). These imaginary components have a associated phase (complex numbers can be written in polar form). It is the phase differences of these off-diagonal elements which produces interference (for more details, see this extract from the book Quantum Mechanics Demystified here). The off-diagonal elements are characteristic of a pure state. A mixed state is a classical statistical mixture and therefore has no off-diagonal terms and no interference.
So how do the off-diagonal elements (and related interference effects) vanish during decoherence?
The off-diagonal (imaginary) terms have a completely unknown relative phase factor which must be averaged over during any calculation since it is different for each separate measurement (each particle in the ensemble). As the phase of these terms is not correlated (not coherent) the sums cancel out to zero. The matrix becomes diagonalised (all off-diagonal terms become zero). Interference effects vanish. The quantum state of the ensemble system is then apparently "forced" into one of the diagonal eigenstates (the overall state of the system becomes a mixture state) with the probability of a particular eigenstate selection predicted by the value of the corresponding diagonal element of the density matrix.
Consider the following density matrix for a pure state ensemble in which the
off-diagonal terms have a phase factor of 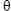 :
:
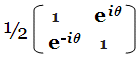
I have written a JavaScript program to show how
the decoherence process averages over the off-diagonal terms of the density
matrix shown above. Click the Start Decoherence button below to
start the sequence. The process averages over the ensemble of particles, each
iteration adding a new particle with a randomly-selected value of 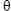 . As each new particle
is added and averaged, the off-diagonal interference terms reduce, eventually
vanishing to zero:
. As each new particle
is added and averaged, the off-diagonal interference terms reduce, eventually
vanishing to zero:
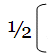 |
1 | 0.7071 +0.7071 i |  |
| 0.7071 -0.7071 i | 1 |
(If you find one of the numbers fails to decrease to zero then it means there has been a rupture in the very fabric of spacetime and the universe will explode in 30 seconds).
Comments
Here you can add your comments about this
article.
Your comments will appear instantly on this page (underneath this
form):
If waves mixing with many other
waves conceals the interference between some particular waves, the change from a
superposition of states to an eigenstate is a process that should IN PRINCIPLE
be possible to determine, meaning (in principle)it should be possible to predict
the outcome of a quantum measurement.
Does decoherence theory formally
define the necessary conditions for determining the outcome of a quantum
measurement?
It seems strange that there should still be an irreducible
probabilistic quality to quantum measurements if deterministic waves are just
mixing with other deterministic waves. - Simeon, 19th March 2007
What an interesting question!
My understanding is that current decoherence theory merely presents an
explanation for the appearance of wavefunction collapse. The Wikipedia site
states this quite nicely: "The quantum nature of the system is simply leaked
into the environment so that a total superposition of the wavefunction still
exists, but exists beyond the realm of measurement."
You make a very
good point, though. If the quantum jump is an illusion or an approximation to
the reality of events at a quantum level, then maybe events at the quantum level
are actually deterministic and we could, in principle, determine the outcome of
a quantum measurement. This all boils down to what is happening in the quantum
"foam" at the smallest Planck Scale (have you read the section on "Veiled
Reality": http://www.ipod.org.uk/reality/reality_veiled_reality.asp
). This is all highly-speculative, and there a few tentative theories. But
decoherence says nothing about this. - Andrew
Thomas, 19th March 2007
Thanks for answering so
quickly. I did read the veiled reality section and have looked at the rest of
the site. It is very good. I especially liked the criticism of renormalization
in particle physics (although my maths is not good enough to understand the
proposed alternative).
It is disappointing that decoherence does not say
anything about determinism.
What are you views on Shariar Afshar's
double slit experiment? - simeon, 19th March
2007
Yes, I considered Shahriar Afshar's double slit experiment wondering if I should mention it on the site http://en.wikipedia.org/wiki/Afshar_experiment The New Scientist magazine has also run a series of articles championing it (rather unwisely I feel). Firstly, Afshar's experiment does seem to be at odds with our understanding of quantum mechanics. However, the fact that there does not seem to be anything particularly remarkable about his experimental set-up (i.e., no special materials or technology involved) makes it unlikely that any new principles are involved. Plus the fact that accurate details of his experimental set-up seem to be in short supply (I've only ever seen basic block diagrams - could mean anything). It's all reminiscent of the "cold fusion" experiment: extraordinary claims from everyday technology. I suspect there's nothing in it at all, so I decided not to reference it on the site. Thanks for your great questions. - Andrew Thomas, 19th March 2007
You are most probably correct
about the Ashfar experiment.
Any views on quantum chaos as a link to a
deterministic QM? - Simeon, 20th March
2007
I've never heard of quantum chaos, sorry. Sounds very interesting. I'll have to look it up. Maybe you can tell us what it's all about? - Andrew Thomas, 20th March 2007
Quantum chaos is the study of the chaotic behaviour of quantum systems. This interests me becuase chaotic behaviour appears probabilistic but is deterministic, and also because quantum systems described by linear wavefunctions should be incapable of nonlinear behaviour, but chaotic quantum systems have been observed. - Simeon, 20th March 2007
That sums it up nicely. Thanks, Simeon. - Andrew Thomas, 22nd March 2007
It seems that, on the section
of decoherence, starting with the sentence, "A system with no diagonal terms in
its density matrix would allow for no interference states." roughly a couple of
paragraphs preceeding the awesome 'javascript' demonstration, you have several
times typed 'diagonal' where you likely meant 'off-diagonal' (unless i am
misundertanding something)....with a couple of exceptions to this comment.
At any rate, much obliged for this exceptionally lucid explanation of
decoherence etc. - patel, 28th March
2007
Thanks for the compliment and finding all those errors (!). I've modified the text - hopefully it's OK now. - Andrew Thomas, 28th March 2007
My work involves molecular systems with tens of atoms up to a few thousand atoms, mostly organic compounds. We model the binding of small molecule compounds to proteins and other macromolecules. We often use quantum calculations to model the electronic structure of the compounds during binding events. I've often wondered if decoherence is a characteristic of these atomic/molecular systems that we should be modeling. In other words, is decoherence related to the number of atoms in a compound? Is decoherence relevant for single atoms, or a small number (ensemble) of atoms, but not for larger collections of atoms? - Richard, 26th April 2007
Hi Richard, take a look at this New Scientist article which describes how researchers at the University of Vienna have passed a buckminsterfullerene molecule through two slits at once: http://www.ipod.org.uk/reality/reality_forever_quantum.asp and they're now talking about doing the same thing with viruses. There's no limit in theory. - Andrew Thomas, 26th April 2007
I notice when I run the "Start Decoherence" simulation, the imaginary terms in the two off diagonal elements tended to reach zero far more quickly than the real terms. Is this a real effect, or just due to the nature of the program you used to generate the simulation? I noticed the real terms in the off diagonal elements sometimes remained measurable for several minutes (measurably >.5) and took a very long time to reach zero (it was around 0.03 after five minutes at which point I gave up watching). - Lionel Sleeper, 27th April 2007
No, it was just my bad programming!! You're absolutely right. Don't take it too seriously - it was just a bit of a novelty. - Andrew Thomas, 27th April 2007
I was puzzled why you think decoherence explains the observation problem. If it were true, it would remove the subjective element from the interpretation of QM. Do you think it is possible to devise an experiment that could separate observation from decoherence. For example, there might be a setup which does not disturb the wavefunction and entanglement with the environment might continue (we already know of one such apparatus - the back screen); we could choose to observe/not observe with such an apparatus, and see what effect results? - Brett Wilson, 28th September 2007
Hi Brett, the quantum
measurement problem is such a puzzle for physicists because the structure of the
wavefunction is defined very precisely by the Schrodinger equation (no
probabilities there) until a "measurement" is taken, in which case we see this
sudden, mysterious, discontinuous probabilistic jump. What constitutes a
"measurement"? What is the reason for these sudden quantum jumps?
Decoherence solves this apparent quantum jumping by revealing that there
is no sudden jump, but rather we see the progressive influence of billions of
particles (in our measuring device) and associated entanglements, each playing a
part in reducing the interference terms in the state vector (a process which
happens incredibly fast) so we apparently get an immediate jump. Jim Al-Khalili
explains this so well in his book "Quantum": "The phenomenon of decoherence
shows that there is no sharp dividing line between the micro and macro worlds,
but rather that the interference effects of superpositions disappear
increasingly quickly with increasing complexity of a quantum system". I've
included the relevant two pages of the book: http://www.ipod.org.uk/reality/reality_alkhalili_decoherence.asp
which also describes an experiment very similar to the one you suggest. -
Andrew Thomas, 28th September
2007
Wonderful page. Very helpful.
Thanks!
I have a question : In what way is the electron an isolated system
while a macroscopic system is not? And why is the coefficient fluctuation time
short for a macroscopic object and long for a microscopic one? In what way is
the environment of a macroscopic object different from that of a microscopic
object? - Bleep, 2nd November
2007
Mr. Bleep: "In what way is the electron an isolated system while a macroscopic system is not?" Imagine an isolated electron in the double-slit experiment, for example. It is not interacting with any other particles. If we want to see where it is, for example, we would have to shine a light on it (hit it with a photon, basically) and then it is no longer isolated, it forms an entangled state with the photon. And if we have a macroscopic measuring apparatus then the electron gets entangled with some other atoms at the front of the probe, which in turn get entangled with millions more particles in the apparatus, and before you know it your electron has become entangled with BILLIONS of other particles - all in the flash of an eye. So that's why - if we can keep our electron isolated - it will not form entangled states and lose its potential to produce interference (as in the double slit experiment). But in a macroscopic system, the sheer number of entanglements will rapidly destroy any interference states of the electron. Hence, the electron very rapidly apppears as a point particle, and we get sayings like: "When we try to detect a wave, we find a wave, and when we try to detect a particle, we find a particle". In fact, it's not an either/or situation: there is a halfway house between the two scenarios but it disappears so rapidly we can never see it! - Andrew Thomas, 2nd November 2007
I was thinking about the great number of air molecules, dust particles, stray cosmic particles etc!! (which could lead to a spontaneous decoherence) So the electron would be isolated only if it were in vacuum? Or why would these interactions be considered negligible...- This was my doubt. - Bleep, 3rd November 2007
Good question, Mr. Bleep. Each particle would have an effect, but, as it says in the text, we need the particle to have a macroscopic effect. Just hitting it with a couple of microscopic particles would not do the trick. Here's another quote from Quantum Enigma: "For a photon bouncing off an atom, there is a clear answer: the photon does not observe the atom. After the encounter, the photon and atom are in a superposition state that can be confirmed with a complex two-body interference experiment." - Andrew Thomas, 3rd November 2007
Some days back, in a response to someone you had posted a link to a page on the density matrix: It had a couple of scanned pages from a book. (Just to help you remember- it had some markings in pink). I found that page really helpful but am not able to trace it now. Can you again please provide the link for the same? Thanks! - Betty, 9th November 2007
Yes, it's from "Quantum Mechanics Demystified" and I moved the link to the main text: http://www.ipod.org.uk/reality/reality_density_operator.asp - Andrew Thomas, 9th November 2007
As I understand, there is a
distinction to be made between "superposition" and "interference", right? While
the "original" sperposition inclides interference terms, these are lost by way
of decoherence, so what is left is similar to a classicla mixture, but you would
still call this a superposition albeit without interfernce? i.e. a superposition
of proper states only?
And whether a given system exhibits interference or
not depends on which observable we consider? For, a given expansion may contain
only proper states of one observable, but not for another. Is this the so-called
problem of preferred basis? - Spark, 12th
November 2007
Hi Spark, thanks for your comment. Make sure you read the other pages including the one on the Quantum Casino: http://www.ipod.org.uk/reality/reality_quantum_casino.asp In a nutshell, before observation we can consider a system to be in a superposition state, and it is possible to generate interference effects from these superposition terms. After observation, the system no longer appears in a superposition - we obtain a single value for our observable. So you would not call that a superposition. The paper by John Boccio contains a good explanation of choice of basis: http://www.ipod.org.uk/reality/reality_boccio.pdf - Andrew Thomas, 12th November 2007
...which means this whole problem of the presence of interference is basis-dependent? In other words, it depends on WHICH observable you measure? If it so happens that you want to measure an observable; in a superposition of whose proper states the system is in, then you directly get a mixture...? - Spark, 12th November 2007
Thanks for your quick response!
1. My second comment was posted before I saw your response
2. I am NOT
talking of the post-observation scene, but the pre-observation scene.
My
point was about pure and mixed states- both states can be represented by the
same superposition (only, the very nature of a system in a pure state is
different from that of a mixed state, but the statistical outcomes of
random-picking members from both types of ensembles is the same) And according
to decoherence, a pure state is changed to a mixed state. So my question was,
this mixed state is also infact a superposition (of proper states only) right?
Since it is a fact that decoherence does not tell you WHICH eigenstate you'd end
up with, it does not solve the problem of a system being in a superposition
(albeit a mixture), but only that of a system exhibiting interference. Is this
correct? Each member of the ensemble in a mixture has a definite state, so would
we then have to invoke multiple observers- each associated with each of the
members of the ensemble? Is this where the many worlds/ many minds theories
enter? - Spark, 12th November
2007
Here I use "superposition" in the sense of a linear combination. - Spark, 12th November 2007
Hi, "pure and mixed states- both states can be represented by the same superposition" - no, pure and mixed states are different superposition states - as you say "the very nature of a system in a pure state is different from that of a mixed state". They are different. They can APPEAR the same after measurement, depending on your choice of basis (that John Boccio paper is very good on explaining that). However "statistical outcomes of random-picking members from both types of ensembles" CAN be different (as explained in the Boccio paper). I don't think you're quite getting what a superposition state is. We never see a superposition in the real world - a superposition is a cat alive and dead at the same time. That would be a pure state - we never see that in the real world. If we have two cats - one dead and one alive - then that's a mixed state. It's not a superposition state, as you suggest. We can see the two cats in the real world. Your comment: "it does not solve the problem of a system being in a superposition (albeit a mixture)" - but if you've got a classical mixture, a dead cat and a living cat, you don't NEED decoherence. You just find one cat alive and one cat dead after measurement. A key thing you seem to be missing is that a mixture is a CLASSICAL mixture, like coloured billiard balls in a bag. It's the situation we are used to in our classical reality. No quantum effects. You don't need multiple observers as you suggest, just one observer pulling the balls out of the bag (cats out of the hat). - Andrew Thomas, 12th November 2007
And by using the word "superposition" in both the case of a pure as well as a mixed state, I mean while in the former each member of an ensemble is in a superposition, in the latter the ensemble as a whole is in a superposition which does not represent the state vector for the system. - Spark, 12th November 2007
Have a read of my previous comment - you're not quite grasping the concept of a superposition. - Andrew Thomas, 12th November 2007
The problem is, we are not
talking about a REAL ensemble, are we? I thought Born introduced the idea as a
purely interpretative aid. Surely, we are not going to be preparing an ensemble
of identical object-apparatus set-ups and carrying out measurements on all of
them, are we? So by "superposition" in the mixed state case, i meant the
ensemble as a whole is in a superposition. (As given in the boccio paper: the
expression for psi of the box as a whole) Sorry for the confusion. But I see, we
probably cannot use the term "superposition" for the ensemble as I thought.
With the result of measurement still being uncertain (we dont know WHICH
eigenstate will result) even after using decoherence theory, each observer
associated with each member of the object-apparatus ensemble will record a
different value depending on the probability associated with that eigenstate. So
WHERE are these observers and their object-apparatus units? Is each in a
different world? - Spark, 12th November
2007
Yes, for discussion about the
density matrix we're talking about a real ensemble - a statistical
interpretation - see http://en.wikipedia.org/wiki/Ensemble_Interpretation
Einstein liked it because he could not come to terms with superpositions and
felt the statistical interpretation held all the answers - from that Wikipedia
page: "the state vector would not apply to individual cat experiments, but only
to the statistics of many similar prepared cat experiments." So, yes, "we ARE
going to be preparing an ensemble of identical object-apparatus set-ups and
carrying out measurements on all of them" - but only for discussions about the
statistical density matrix formulation. Decoherence as such can apply to a
single observation, in which case the density matrix (being a statistical
device) is not relevant. Statistics only apply to multiple measurements. As
described in the main text, the great value of the density matrix is that it can
describe a system which cannot be represented by a single state vector (i.e., an
ensemble of particles in a mixed state).
Your final point refers to the many
worlds interpretation (which I don't believe). Many worlds was an attempt to
understand the apparent random "quantum jump" to an eigenstate by saying
different observers in parallel universes record different values. I think
decoherence removes the need for parallel universes - the interference states
just dissipate (as explained in the text), they don't need a parallel universe.
Though this is just my opinion. People are inventing multiverses for any problem
they don't understand! - Andrew Thomas, 12th
November 2007
How would decoherence be explained for a single system (in which case the density matrix is not involved)? We wouldn't even be able to talk of mixtures. Then, what? - Albert, 18th November 2007
You're right, the system would then be in a pure state: http://en.wikipedia.org/wiki/Pure_state a superposition state. But the interference terms present in the pure state would vanish into the environment when we take a measurement, so we only see the one eigenstate. The probability of which eigenstate we see is determined by how close the state vector is to a particular eigenstate: "Basically, the nearer the current state is to a particular eigenstate, the more likely it is to jump to it" - see http://www.ipod.org.uk/reality/reality_quantum_casino.asp - Andrew Thomas, 18th November 2007
Can the state vector
representation in Hilbert Space be considered a kind of phasor diagram? Do the
angles between the vectors represent phase differences between the corresponding
matter waves?
In the superposition diagram in your text, the eigenstates
seem to be orthogonal. In fact, basis states are orthogonal if I'm not wrong.
(For eg., a 2 state system where the 2 states span the entire space) This being
the case, how can orthogonal components show superposition/ interference? Isnt
orthogonality of components a condition that arises only when decoherence
happens?? - Sindhuja, 18th December
2007
That's an interesting point you
make about a phasor diagram (like in an alternating electric current), but, no,
my understanding is the Hilbert space is more complicated than that. The Hilbert
space is a **complex** space, but don't get that mixed up with some sort of
Argand diagram with an imaginary component being orthogonal to a real component.
Whereas the components of a normal vector space are all real numbers, in a
Hilbert space all the components can be complex numbers - it's very hard to
imagine ("The differences between Hilbert space and phase space are important.
Hilbert space is a multi-dimensional complex projective ray space" - http://www.qedcorp.com/pcr/pcr/hilberts.html
"The lengths of the vectors can be complex numbers" - http://alumni.imsa.edu/~matth/quant/433/shor-par/node6.html
)
Regarding your point on eigenstates, eigenvectors with different
eigenvalues are always orthogonal. So we can think of the eigenstates as forming
the basis vectors, and a superposition vector is then a combination (mix) of
those possible eigenstates. Wikipedia says it well: "The observable has a set of
eigenvectors which span the state space. It follows that each observable
generates an orthonormal basis of eigenvectors (called an eigenbasis).
Physically, this is the statement that any quantum state can always be
represented as a superposition of the eigenstates of an observable." http://en.wikipedia.org/wiki/Measurement_in_quantum_mechanics
- Andrew Thomas, 18th December
2007
Right...thanks.
But, http://www.geocities.com/Athens/Acropolis/1756/everett.txt
(the third paragraph in the answer to Q6) gives orthogonality as a condition
arising from decoherence in which case there cannot be "a significant degree of"
overlap of components, which as I understand, precludes the possibility of
superposition. But as you say, eigenstates with different eigenvalues are always
orthogonal.So what is the between this fact and the statement that "components
become permanently orthogonal" when decoherence happens?
(I am disregarding
any mention made to "worlds" in the link I've given) - Sindhuja, 18th December 2007
Hi Sindhuja. You understand that a quantum system can always be described by a single state vector? Before decoherence, the system can be in a superposition state, in which case the state vector will be a linear superposition of several orthogonal state vectors (my second diagram "a superposition state expressed as a sum of components of other states" shows this clearly). After decoherence, the state vector can be represented by just ONE of those component eigenvectors (see my third diagram "The system state appears to be in an eigenstate"). That quote in the link you gave "components (or vectors in the underlying Hilbert state space) have become permanently orthogonal" is wrong - the component vectors are ALWAYS orthogonal. - Andrew Thomas, 18th December 2007
Doesn't this page (whose link
you've provided in the text) also say the same thing? http://www.mulhauser.net/research/tutorials/decoherence/index.html
"Simplifying
hugely, the probability of randomly selecting two wavefunctions in a high
dimensional Hilbert space which are not orthogonal is vanishingly small. So long
as there is even a very small coupling between an object and its environment,
this tendency of wavefunctions for the environment rapidly to become orthogonal
means coherent phase relationships between macroscopically distinct states are
destroyed, off-diagonal terms of the reduced density matrix vanish, and
interference effects become impossible."
How can it be that it is MORE
LIKELY to pick 2 state vectors that are orthogonal in a HIGH dimensional space
(resulting from entanglement and leading to decoherence) if they are ALWAYS
orthogonal?
Is non-orthogonality of vectors a condition at all for
superposition?! My understanding was that it is not, as you'd said in the
earlier post as well as in the text. - Sindhuja, 18th December 2007
Hi Sindhuja, you still don't seem to be distinguishing between a state vector and components. Components are not a state vector. A state vector is a single vector describing a state which can be in any direction. Components FORM the state vector. As I said, see my second diagram "a superposition state expressed as a sum of components of other states". Components are always orthogonal. I didn't say state vectors are always orthogonal - I said components are always orthogonal. This is where I think you're going wrong - you seem to be confusing component vectors and the state vector. In general, a system has a single state vector which can be decomposed into many orthogonal component vectors (that Mulhauser paper is written in a rather confusing manner - he is referring to the density matrix representation, which I consider at the end of my article). - Andrew Thomas, 19th December 2007
What interference are we
talking about? That between component (eigen)vectors or that between state
vectors?? You say for two component vectors to combine in a superposition they
must be in phase; Wikipedia http://en.wikipedia.org/wiki/Quantum_decoherence
gives possibility of a scalar product as a condition for "overlap" or
interference. But evidently, the scalar product ("closeness")of two orthogonal
vectors is zero and so they should not be able to interfere according to this
condition.
It is very confusing as to what interference we are talking
about. - Sindhuja, 19th December
2007
That Wikipedia article is very
confusing - badly written and wrong in places (you seem to have a knack for
finding bad articles on the web!). My main text treats it as clearly as I can.
Before observation, a particle can be in a superposition state (for example, a
particle in the double-slit experiment will produce an interference pattern).
When a state vector is in a superposition, it can have many orthogonal component
vectors (see my diagram on the superposition state). These represent
interference states - other eigenstates. For example, in the double-slit
experiment those intereference states might represent other possible positions
for the particle.
But after an observation is taken (e.g., the particle
hits the screen) each component vector of that particle will get entangled with
the environment. The result of the random entanglements with random phases is
that those interference states dissipate into the environment (disappear). Those
interference component states disappear, and we are only left with the single
eigenstate state vector. Hence we see a single particle position. - Andrew Thomas, 19th December 2007
