The Cosmic Universe
This page considers some of the key issues in cosmology, the science that attempts to grasp the biggest picture of all: how did the universe start, where is it going, and was there anything before?
The Origin of the Universe
In 1970, Stephen Hawking and Roger Penrose showed that general relativity predicted that the universe would have started with a singularity, a single point with infinite density and infinite curvature of spacetime (see the Penrose-Hawking singularity theorems). This might sound like an elegant and compact solution to how the universe started. However, this poses a problem for physics as our current models break down at infinite densities (this is nicely explained here). For example, if we attempt to calculate the initial density of the universe:

In this case we have complete freedom to choose any initial conditions for the universe. So the situation can be summed-up as: anything can happen at a singularity. Again, this might appear to be an elegant, compact solution to how the universe started. But if the universe really did begin with a singularity that would render the situation beyond mathematical analysis (fortunately, we don't generally find infinities in physical reality, and the presence of infinities in a theory is usually taken as a sign that the theory is flawed). The result has been a succession of imaginative ideas by which the singularity at the start of the universe might be avoided.
In 1973, Edward Tryon proposed the theory that the universe (as a small point
- a quantum particle) might have emerged out of nothing (ex nihilo
creation) due to a quantum fluctuation. According to the Heisenberg
uncertainty principle, there can be enough uncertainty about the energy at a
point, 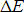 , to allow the creation of a particle/antiparticle pair, but only
for a very short time,
, to allow the creation of a particle/antiparticle pair, but only
for a very short time, 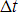 :
:
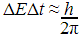
In 1982, Alexander Vilenkin extended Tryon's proposal to consider the idea that the universe could have inflated from one of these "virtual particles" (see here). Andre Linde realised that a succession of further quantum fluctuations within the expanding universe would result in areas of secondary inflation. This process can continue indefinitely in a process known as eternal inflation. In an eternally inflating universe, "bubble" universes can bubble-up out of an eternally inflating space like bubbles in a bottle of champagne (see Andrei Linde's arXiv paper hep-th/0211048).
Inflation is now generally accepted as describing conditions in the earliest moments after the origin of the universe. But inflationary theories should not be considered as providing the "whole story" of the origin of the universe: inflationary theories do not seem to avoid the initial singularity, as Stephen Hawking point out on page 52 of his arXiv paper hep-th/9409195: "Inflation alone can not explain the present state of the universe. One can see this by taking any state for the universe now and running it back in time. Providing it contains enough matter, the singularity theorems will imply that there was a singularity in the past." (see also Neil Turok's article Inflation and the Beginning of the Universe).
"Hidden Variables" Theories
(or "How to get something from nothing")Another problem with these inflationary theories is that it might be said that the quantum fluctuations do not really emerge out of "nothing". As J. Richard Gott says in his book Time Travel in Einstein's Universe: "Making the universe out of literally 'nothing' seems difficult. How does 'nothing' know about the laws of physics? After all, any tunnelling-from-nothing model starts out with a quantum state obeying all the laws of physics - and that is not nothing. Indeed, trying to make the universe out of nothing may be considered odd, since 'nothing' is something that, by definition, would appear not to exist".
This theme is continued in the section "There is no such thing as nothing" towards the bottom of the Quantum Reality page. In that section it is explained how these "virtual" particles in fact appear out of a quantum vacuum. That vacuum has a quantum state (the ground state) and can thus be described by a wavefunction. With this in mind, whether you think the particle actually appear out of "nothing" or not will depend on your opinion about the "ontological status" of the wavefunction: whether you think the wavefunction is just a mathematical tool for calculating probabilities or, in fact, describes something "real", an underlying structure.
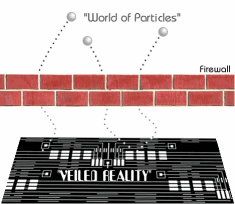
Diagram from the Quantum Reality page
This was all described in detail on the Quantum Reality page which proposed the idea of a "veiled reality" layer as a means of explaining counter-intuitive quantum behaviour such as non-locality (instantaneous connections over great distances - an effect which seems to be ignored in quantum cosmology). The veiled reality layer could also explain quantum particle production out of "apparently nothing". The veiled reality layer was proposed as describing a "world of wavefunctions", completely hidden from our eyes and our measuring apparatus which inhabit a "world of particles". This would explain how virtual particles appear "out of nothing": the appearance and disappearance of particles is controlled by the veiled reality layer. The veiled reality layer is certainly not "nothing", but the truth is hidden from our particle-oriented eyes.
(The "Pilot Wave" hidden variables theory of David Bohm is also described on the Quantum Reality page, though the pilot wave only controls the position of particles: "Bohmian mechanics does not account for phenomena such as particle creation and annihilation characteristic of quantum field theory" - see the last paragraph of Stanford Encyclopedia of Philosophy. However, a hidden variables theory could be generated which also controls the creation of particles in the manner described above.)
Causal Loop Theories
Let's imagine what sort of objects could appear out of nothingness. It would appear that only those objects which could create themselves could come into existence. But what sort of objects can create themselves? And, most importantly, could our very universe have created itself?
Theories which seem most successful at avoiding an initial singularity seem to those which involve some sort of looping in time, or "curving" of spacetime. These theories seem to have the advantage of theories involving linear time which inevitably lead back to an initial singularity. Also, some of these "curvy" theories seem to propose a universe which can, indeed, "create itself", thus providing an all-important motive for our existence.
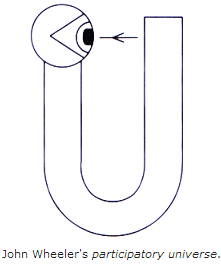
John Wheeler has proposed a model for a participatory universe which would appear to belong to this category of "universes which could create themselves". The principle of the participatory universe is summed-up by Martin Rees: "The universe could only come into existence if someone observed it. It does not matter that the observers turned up several billion years later. The universe exists because we are aware of it." In this sense, the participatory universe borrows strongly from the quantum mechanics interpretation that "observation creates reality" - by observing the universe, we somehow bring it into existence. However, I (in common with the majority of physicists) do not subscribe to the controversial "conscious observation creates reality" interpretation of quantum mechanics (see the page on Quantum Reality for my reasoning).
What other possibilities are on the table? I prefer examples which create themselves through some sort of causal loop. For example, in the film The Terminator a robotic killing machine (Arnold Schwarzenegger) is sent back in time to kill a rebel's mother before the rebel is born. The terminator is defeated, but some of his advanced technological body parts are retained, and it is the technological advances which result from examining those body parts which allow future scientists to construct the Terminator. So nobody actually invented the technology used to construct the Terminator! (I'm convinced this is the technique Apple used to develop the amazing new touch-screen iPods!). An object such as this which is "invented out of nothing" by a causal loop is called a jinn.

As strange as this may sound, there is no logical inconsistency here. There is nothing in physics to say this is not allowed: nothing both happens and doesn't happen. And if the technique can produce something as complex as the Terminator from nothing then maybe it could also produce a universe from nothing.
J. Richard Gott has suggested a method for a universe to create itself if it formed a causal loop in spacetime (see here). His principle imagines an extreme curvature of spacetime forming a wormhole, allowing time travel to the past. The diagram below shows the loop in time:

There is another possible causal loop solution which would also explain anthropic fine-tuning. Maybe an advanced (human?) civilisation in the future could travel back in time to create the universe which they knew would evolve themselves into existence. Such a process would explain fine-tuning because they would have to set the parameters very precisely to ensure their particular civilisation and its inhabitants would result.
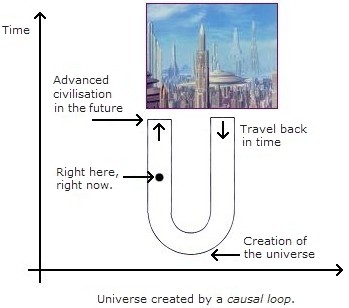
This idea is considered by J. Richard Gott on page 191 of his book Time Travel in Einstein's Universe: "With a time-travel loop, an intelligent civilisation could produce the trunk as well". This ties in with the work of Farhi, Guth, and Guven who proposed that baby universes could be created in the lab by an advanced civilisation (see the page on The Big Brother Universe).
The "No Boundary" Proposal
Another "curvy time" solution is the "No Boundary" proposal of Stephen Hawking and James Hartle.
As we trace the universe back in time to the singularity we not only find our laws of physics breaking down, but we are also left with the apparently unanswerable question of "what happened before the Big Bang"?
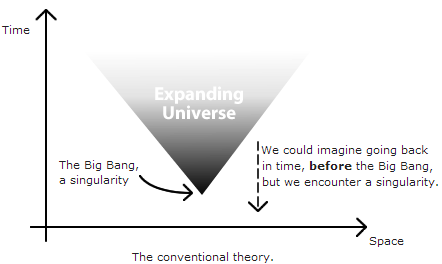
In 1981, Stephen Hawking and James Hartle came up with an imaginative proposal which promised to avoid the singularity at the origin of the universe, and also gave a answer to the question of why there was no time before the Big Bang. But before we can consider the theory, we need to introduce a couple of concepts.
Firstly, we need to introduce the idea of a metric, which is a way of defining distance. In our (x, y, z) three-dimensional space, the formula for distance is provided by Pythagoras's theorem:
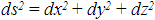
When we extend this notion to 4-dimensional spacetime, it might be imagined that the time axis is treated the same way (creating the Euclidean or Riemannian metric):
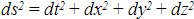
However, Einstein's theory of special relativity says that the clock which travels the furthest actually shows the smallest time measurement, not the largest. So we need to use the Lorentzian metric (the "time" element becomes negative):
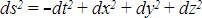
Hartle and Hawking's proposal was to employ a mathematical transformation called a Wick rotation to modify the time axis to avoid the singularity. In the Wick rotation, the time axis is multiplied by the imaginary number i (the square root of minus one), in which case the Lorentzian metric is converted to a Euclidean metric:
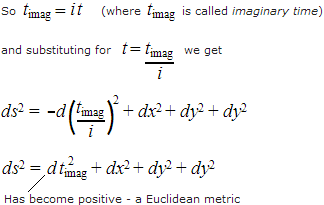
As a result of the Wick rotation, the time axis is converted to a complex number. The time axis is rotated 90° anticlockwise from the original time axis to become the imaginary time axis:
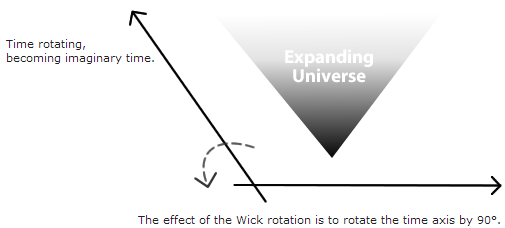
The following diagram shows the resultant graph rotated by a further 90° (but this time clockwise) so that the imaginary time axis now points in the vertical direction - taking the place of the old time axis:
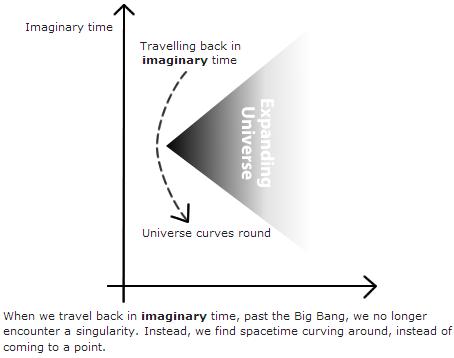
It is as though when we travel back in time we find time itself curving round so that spacetime forms a smooth surface, instead of coming to a point singularity:
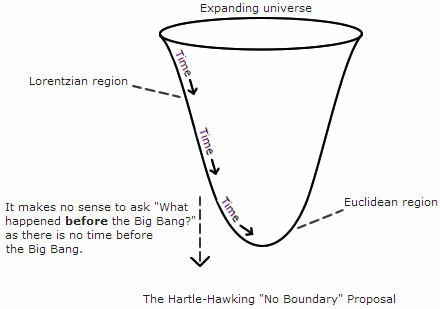
So how can the No Boundary proposal answer the question: "How did the universe appear out of nothing?" Well, it would say that the question is flawed. According to the No Boundary proposal, there is no time before the start of the universe, time is self-contained within the universe. So nothing could have created the universe: it just is. It just "exists", essentially for no reason.
For me, this doesn't answer the question "Why?": "Why should the universe exist at all instead of not existing?". I feel this rather passive universe, lacking any form of motive its existence means the No Boundary proposal is not as compelling as theories in which the universe is an object capable of creating itself (such as the causal loop theories presented above). At least those theories answer the question "Why does the universe exist instead of not existing?".
For more details on the No Boundary proposal, see chapter 3 of Stephen Hawking's arXiv paper hep-th/9409195. There is also a series of video lectures on this subject by Stephen Hawking on YouTube:
- Origin of the Universe - Stephen Hawking (1 of 5)
- Origin of the Universe - Stephen Hawking (2 of 5)
- Origin of the Universe - Stephen Hawking (3 of 5)
- Origin of the Universe - Stephen Hawking (4 of 5)
- Origin of the Universe - Stephen Hawking (5 of 5)
Quantum Gravity: The Wheeler-DeWitt Equation
Quantum cosmology is the attempt to find a fully quantum mechanical description of the large-scale universe and to explain the origin of the universe. In order to study the universe in this way, we need to examine spacetime - the underlying substrate which seems to compose the universe. Because gravity is treated as a curvature of spacetime itself (in Einstein's theory of general relativity), most quantum cosmology theories are based around trying to find a quantum theory of gravity: quantum gravity.
A great puzzle in physics has been how to reconcile Einstein's theory of general relativity with quantum mechanics. General relativity remains our main theory for describing gravity, and is extremely accurate for with large objects (stars and planets, etc.). Quantum mechanics, on the other hand, is our main theory for dealing with microscopic objects, and the other three fundamental forces which act at the atomic scale (see the It's a Small World page for a description of those other three fundamental forces). General relativity describes space as being a smooth surface, but quantum mechanics reveals a discontinuous microscopic world with constant fluctuations and activity. So, each of these theories is accurate in its own right but they describe the nature of space and matter so differently that it has proven highly problematic to combine the theories into a single unified theory.
But perhaps there is an even more fundamental difference between the two theories. Quantum mechanics attempts to describe the behaviour of particles as they move within a universe composed of spacetime. However, a theory of quantum gravity would seek to describe the behaviour of that background spacetime itself. They seem to be two different entities, and we, as yet, have no evidence that it is valid to apply the principles of quantization to spacetime. This question will be considered later on this page.
Before we consider quantum gravity, we need to introduce the concept of the Lagrangian. The Lagrangian is a reformulation of classical mechanics, i.e., it is a different approach to describing the motion of a system. The Lagrangian allows us to describe the complete motion of a system - however complex, however many objects it contains - by a single equation: the Lagrangian. The Lagrangian is defined as the kinetic energy of a system minus its potential energy. The Lagrangian is defined for all possible configurations of all elements of the system, so it is possible to plot the Lagrangian as a surface in space (more accurately, an N-dimensional manifold):
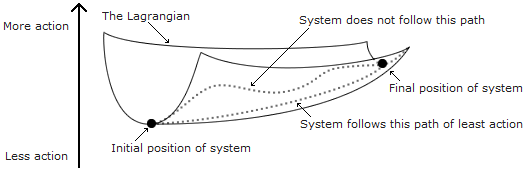
It can be shown that the state of the system as it moves from point A to point B along the Lagrangian follows the path of least action (in other words, the shortest distance between the two points - see here). This essentially means that nature wants to convert potential energy to kinetic energy (or vice versa) by the most efficient means possible with respect to time. In the diagram above, it can be seen that the state of the system moves along the base of the trough between the start and end points - the shortest distance between the two points. The Lagrangian is such a powerful tool as once you have managed to find the Lagrangian for a system you know precisely how it will behave: it will follow the path of least action. The Lagrangian alone is enough to describe the system. For this reason, in modern fundamental physics, when some new theory is proposed, it is almost invariably given in the form of a Lagrangian ("For reasons as yet utterly mysterious, this quantity stays as small as possible under all circumstances. Theorists are convinced that action must be incredibly important - so much so that the discovery of any new fundamental law prompts a race to work out the particular action needed to produce it. The trouble is that no one understands the principles behind nature's infatuation with action." - quoted from this New Scientist article).
The Hamiltonian is closely related to the Lagrangian, but instead of the difference between the kinetic and potential energy of a system, we now consider the sum of the kinetic and potential energy. To be precise, the Hamiltonian is the sum of the kinetic and potential energy of a closed system expressed in terms of momentum, position, and time (see here).
Now let's see how the Hamiltonian was used to produce the very first results of quantum mechanics. Consider the case of a single particle of mass m moving in some external field given by a potential energy function, V, which can depend on position: V=V(x,y,z).
The (classical) Hamiltonian is the sum of kinetic plus potential energy. Let's derive it:
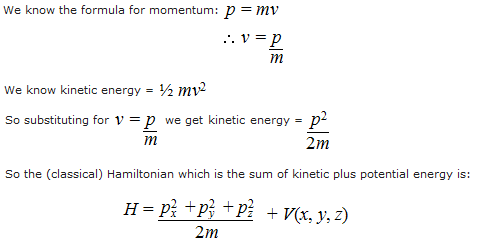
where px, py, and pz are the spatial momenta in the direction of the Cartesian x, y, and z axes.
Now, in order to convert this Hamiltonian to its quantum mechanical form, the momentum variable in this equation is replaced by the result for quantum momentum (which we derived earlier on the Quantum Casino page):
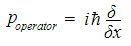
As this is a momentum operator, we need something for it to
operate on. So we have to again introduce this strange concept
of a wavefunction, 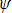 ,
extending through space. Our equation for the Hamiltonian
operator (there is now a circumflex over the H) now
becomes:
,
extending through space. Our equation for the Hamiltonian
operator (there is now a circumflex over the H) now
becomes:
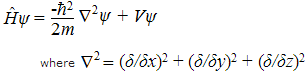
The Hamiltonian, H, is really the total energy, E, so the Hamiltonian operator is the energy operator. But we already derived an expression for the energy operator on the Quantum Casino page:
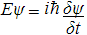
So substituting for this value, our equation now becomes:
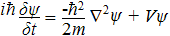
which is the famous Schrödinger equation! This Hamiltonian approach is how Erwin Schrödinger first derived the equation in his 1926 paper "Quantization as an Eigenvalue Problem" (original German paper here).
In 1965, John Wheeler and Bryce DeWitt wondered what would happen if you applied this "standard" method of quantization (called canonical quantization) to the force of gravity. Let's see what happens:
The first principle to note is that of general covariance (sometimes called diffeomorphism invariance). According to the principle of general covariance, a theory must give the same results not matter how you move its coordinate system around in the universe (general covariance arose from the requirements of general relativity). To put it another way, general covariance says that no set of coordinates is special: there is no absolute coordinate system, everything is relative. It can be seen that general covariance inevitably arises from another very simple principle: there is nothing outside the universe, or, to put it another way, there are no absolute axes of reference for space or time outside the universe by which we can make our measurements.
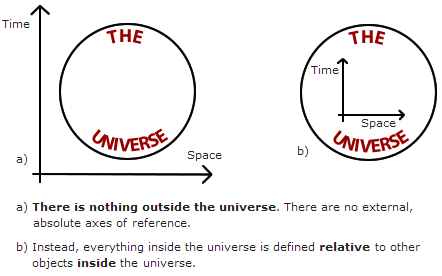
Hence, it is impossible to define a position for our "universe object" (and hence no potential energy) and it is impossible to define a speed (and hence no kinetic energy). The Hamiltonian allows a plot of the variation in total energy of a system as the components of a system take different configurations (e.g., galaxies moving around in our "universe object"). So in this case, the Hamiltonian (kinetic + potential energy) is zero:
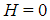
If we are going to quantize gravity using the canonical quantization method, we need to convert this Hamiltonian to an operator (as described in the derivation of the Schrödinger equation above). But if we're converting the Hamiltonian to an operator, we once again need something for it to operate on: we need a wavefunction. So another new concept must now be introduced: the wavefunction of the universe. The principle of the "wavefunction of the universe" imagines the entire universe as a single object, a quantum object. Michio Kaku explains it well: "When the universe was born, it was smaller than an electron, which is a quantum object that can exist simultaneously in many states. So the universe must also be a quantum object and exist in many states." (see here). Whether it is valid to consider the entire universe as a single object subject to the laws of quantum mechanics we shall consider in a later section on this page, but for now we can apply our Hamiltonian operator to our "wavefunction of the universe":
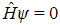
This is the Wheeler-DeWitt equation - a sort of Schrödinger equation for the gravitational field. It is the most famous equation in quantum gravity.
(A variation on this canonical quantization of gravity eventually leads to the recent, highly-speculative field of loop quantum gravity - see this Physics World article by Carlo Rovelli).
Time and the Wheeler-DeWitt Equation
There's something remarkable about the Wheeler-DeWitt equation, and it can be seen if we expand the Hamiltonian operator:
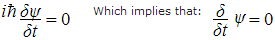
Or, expressed in words, the rate of change of the state of the universe with respect to time is zero. The universe isn't changing with time! But we look around us and we see things changing all the time: people are walking, birds are flying. So is the equation wrong? Well, no. What the equation is once again telling us is that there is no external time reference by which we can measure the progress of time within the universe: there is no clock outside the universe! As Andrei Linde explains: "The notion of evolution is not applicable to the universe as a whole since there is no external observer with respect to the universe, and there is no external clock that does not belong to the universe" (see page 25 of Andre Linde's arXiv paper hep-th/0211048).
The Wheeler-DeWitt equation suggests a model in which all of time is laid-out (just as the space dimension is laid-out), and all times are equally real: there is no special "now", no distinction between past and future. In fact, "past" and "present" do not exist - the movement of time is considered to be just an illusion of human perception (the Wheeler-DeWitt equation reveals how the universe does not change with time as there is no external time reference by which we can measure the progress of time within the universe: there is no clock outside the universe).
Most physicists would favour this model as the most accurate representation of time. It is also called block time because all of spacetime can be viewed as being laid-out as an unchanging four-dimensional block:

For more information about this, see this Scientific American article by Paul Davies.
Eternal Life
It might come as a surprise that this orthodox "block universe" view of time in fact leads us to conclude that we possess a form of eternal life! This is a consequence of the principle that in the block time model all periods of time are equally real. If a loved one dies, you might take some comfort from the knowledge that this period of time in which your loved one is dead has, in fact, no greater reality than the time when your loved one was alive. According to physics, it is just as valid to consider your loved one as alive as it is to consider them dead!
Einstein took comfort from this knowledge when his lifelong friend Michele Besso died. He wrote a letter consoling Besso's family: "Now he has departed from this strange world a little ahead of me. That means nothing. People like us, who believe in physics, know that the distinction between past, present, and future is only a stubbornly persistent illusion."
Of course, the flip-side is that you're already dead!
The Wavefunction of the Universe
In our discussion on quantum gravity we have introduced the concept of a "wavefunction of the universe". The idea is that the universe has a corresponding wavefunction which describes the probabilities of it having different states (forms). This is meant to be analogous to the well-established formulation in quantum mechanics whereby a quantum particle has a corresponding wavefunction which describes the probabilities of it appearing in a certain location, say. Michio Kaku explains it well: "When the universe was born, it was smaller than an electron, which is a quantum object that can exist simultaneously in many states. So the universe must also be a quantum object and exist in many states." (see here). The idea of a wavefunction for the universe was first proposed in the Hartle and Hawking "No Boundary" proposal, though it has since been used in many models of quantum cosmology.
However, it is possible to imagine several objections to this belief that the entire universe can be treated as if it was a quantum particle. In his online physics textbook Motion Mountain, Christoph Schiller draws attention to the many differences between the universe and a particle. He comes to the conclusion that there can be no such thing as a wavefunction of the universe: "Beware of anybody who claims to know something about the wavefunction of the universe. Just ask him: If you know the wavefunction of the universe, why aren't you rich?" (see page 835 of Motion Mountain).
Schiller's first complaint is that the universe cannot have a "state" because a "state" is defined as being the form of a system at a given time. However, that would appeat to require some aspect of the universe to be able to change with time when the universe is viewed "from outside", i.e., the universe could appear to change when viewed by some form of external observer. However, as we discovered earlier in our discussion on quantum gravity, there is nothing outside the universe, certainly no external clock by which changes in the universe might be measured (this unchanging universe was revealed by the Wheeler-DeWitt equation in the previous section).
This idea of a state as being the form of a system at a particular moment in time is even used (perhaps unwittingly) by Stephen Hawking in a description of the wavefunction of the universe on page 43 of his arXiv paper hep-th/9409195: "It is useful to introduce a concept that can describe the state of the universe at one time" (emphasis added). But we know that the wavefunction is not dependent on time! There's no external time axis. So when we talk about a "wavefunction of the universe" we are really considering a "block universe" state in which all of time is laid-out and all times are equally real (see the previous section and the section on "Time" on page 11 of Carlo Rovelli's arXiv paper gr-qc/9903045 which considers this time-independent notion of "state").
We can also see that Michio Kaku's previous convincing quote falls into the same trap by inferring some notion of time external to the universe (by his use of the word "simultaneously" implying some sort of external time reference):

The basic idea behind Michio Kaku's logic is that the universe, being composed of particles which obey the laws of quantum mechanics, could itself be considered a quantum object. This is fair enough. But an anology which treats the universe as though it is an actual particle is unfortunate: the entire universe can never behave in the same way as a particle. As was revealed earlier, there is nothing outside the universe, no external axes, so a "universe particle" can never have a location, or a momentum - both of which are mainstays in the quantum behaviour of a particle. Likewise, we cannot think of the universe as having a "time" (as shown by the Wheeler-DeWitt equation) or an energy ("the energy of a closed universe is equal to zero" - quoted from Alexander Vilenkin's arXiv paper gr-qc/9302016). So we should never think of the universe as a particle, in a quantum superposition (as Michio Kaku suggests). If you need proof, try using that "universe particle" in the double-slit experiment! Where would you get the slits from?!
So if we shouldn't think of the universe as a particle, how should we imagine it? Surely when we are considering the wavefunction of the entire universe as a whole then we should not be just considering it as a single point-particle moving around in a background of spacetime. Surely we should consider it as "the collection of all matter and radiation, plus all of spacetime" (see page 835 of Motion Mountain). But is it valid to apply quantization techniques to spacetime itself? I think an answer can be found if we remember that before we observe a particle's position, we have to consider it to be in superposition of many different possible positions. We should then remember John Wheeler's description of general relativity: "Matter tells spacetime how to curve, spacetime tells matter how to move". If that is the case, then when a particle is in a superposition state we should also consider spacetime (the shape of which is determined by the position of the particle) to be in a superposition state! This implies that it is valid to apply the standard quantum mechanical formulation to spacetime (and, therefore, gravity), and it hence is also valid to consider a "wavefunction of the universe". When we quantize gravity we are quantizing the gravitational field and spacetime which forms the very essence of the universe itself (for more on this, see Carlo Rovelli's arXiv paper gr-qc/9903045).
Decoherence and the Wavefunction of the Universe
If we're now considering the entire universe to be a single quantum system, a superposition state described by a wavefunction, then we might wonder why we do not see superpositions in reality. For example, why do we see not see galaxies in a superposition state like Schrödinger's Cat, dead and alive at the same time, so to speak. The process by which classical states emerge from quantum superpositions is called decoherence, and this is considered in depth in the page on Quantum Decoherence.
Stephen Hawking considers this a likely solution on page 57 of his aforementioned arXiv paper hep-th/9409195: "People normally try to account for decoherence by interactions with an external system, such as a heat bath, that is not measured. In the case of the universe, there is no external system, but I would suggest that the reason we observe classical behaviour is that we can only see part of the universe." I believe this emphasis on an external environment in order to achieve decoherence is rather a misconception. As discussed at the top of the Quantum Decoherence page (the discussion on rainbows), the crucial factor in decoherence is that the object being measured, together with the measurement apparatus, should be considered as one entangled system. The emphasis is on the fact that we should consider the resultant entangled system as being a single system. And this is how we should think of the universe as a whole: one entangled system. There is no need to postulate any external environment. A galaxy, for example, would decohere by its interactions with the other galaxies which surround it.
Comments
Here you can add your comments about this
article.
Your comments will appear instantly on this page (underneath this
form):
Be the first to post a comment!
